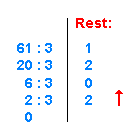
Zehnerzahl 61 ins 3er-System umwandeln: - man dividiert 61 durch 3 - schreibt den Rest 1 schreibt daneben - schreibt das Ergebnis 20 darunter - verfährt entsprechend mit 20, usw. Die Reste, v.u.n.o. gelesen, ergeben die Dreierzahl 2021
Das Plus - Zahlensystem: neuartige Zahlensysteme
Die üblichen Zahlensysteme
Wie funktionieren die üblichen Zahlensysteme? Ein Beispiel: im normalerweise benutzten Zehnersystem (Dezimalsystem) ist die Zahl 222 definiert als:
222 = 2*100 + 2*10 + 2*1 = 2*102 + 2*101 + 2*100 (Jede Zahl hoch Null ist per Definition =1). Entsprechend ist im Dreiersystem (Ternärsystem) die Zahl 222 definiert als: 222 = 2*9 + 2*3 + 2*1 = 2*32 + 2*31 + 2*30 Die Zahl 222 im Dreiersystem bedeutet also dasselbe wie die Zahl 26 im Dezimal- system. 10 bzw. 3 nennt man die Basis des betreffenden Zahlensystems. Zur Unterscheidung schreibt man auch 22210 bzw. 2223
Verbesserungswünsche
An diesen Zahlensystemen könnte ein naiver Betrachter folgendes unschön finden:
- Das Zehnersystem z.B. hat die Basis 10, aber die Ziffern 0 - 9. Wäre es nicht schöner, wenn es die Ziffern 1 - 10 hätte ? - Die Zahl 301 im Zehnersystem z.B. bedeutet 3*100 + 0*10 + 1*1 Könnte man dieses umständliche + 0*10 nicht vermeiden ? - Jede Zahl hat unendlich viele Darstellungsmöglichkeiten mit führenden Nullen (...001) und Nachkomma-Nullen (1,00...) - Selbst bei runden Zahlen ist die Basis des Zahlensystems nicht erkennbar - Bei runden Zahlen 10, 100, ... sind Summe und Produkt der Ziffern immer 1 bzw. 0, ähneln also dem Zahlenwert nicht, und dieser ist nicht rein aus den sichtbaren Ziffern berechenbar ohne Zuhilfenahme der unsichtbaren Stellenwerte
Definition der Plus-Systeme
Wir definieren deshalb eine neue Art von Zahlensystemen, echte Stellenwertsysteme,
und zeigen, dass sie widerspruchsfrei und praxistauglich sind. Definition:
Ein Plus-Zahlensystem mit Basis b (z.B. b=10 oder b=3) verwendet
zur Darstellung von Zahlen ≠ 0 die Ziffern 1 bis b (z.B. 1 - 10 oder 1 - 3).
Die Zahl Null wird mit einer (sonst nicht benötigten) Ziffer 0 dargestellt,
die auch als Dezimalkomma dienen kann (siehe unten).
Es gilt das übliche Stellenwert-System.
Die Bezeichnung "Plus-System" wurde gewählt, weil gegenüber einem üblichen
Zahlensystem zur Basis b ein Plus-System eine höhere Ziffer hat, und weil sich
mit gleichviel Stellen höhere Zahlen darstellen lassen (siehe folgende Tabelle).
Die folgende Tabelle zeigt, wie Zahlen in üblichen Zahlensystemen aussehen
(im 10-er und 3-er System), und wie in den entsprechenden Plus-Systemen:
10 |
In der Tabelle sind die Zahlen, die im Plus-System anders aussehen,
durch eine Notiz dahinter hervorgehoben. Es sind genau die Zahlen, welche die
höchste Ziffer b (= Basis) enthalten, und das sind genau die Zahlen,
welche im "normalen" System eine Null enthalten.
Im Plus-System zur Basis b folgt auf eine Zahl des Typs bbb
(n mal b, die höchste Zahl dieser Länge) die Zahl 1111 (n+1 mal 1,
die niederste Zahl dieser Länge). bbb hat also den Wert 1111 - 1
(= 1110 im normalen Zahlensystem; 1111 hat in beiden Systemen
denselben Wert, da es weder Ziffer 0 noch Ziffer b enthält
und die Stellenwerte gleich sind)
In beiden Arten von Zahlendarstellungen (Plus oder nicht Plus) sind die meisten
Zahlen gleich. Aber je kleiner die Basis des Zahlensystems wird, desto mehr
Zahlen sind verschieden. (Deshalb zeigen wir in der Tabelle auch das Dreiersystem,
weil da der Unterschied deutlicher ist).
In beiden Arten von Zahlensystemen (Plus oder nicht Plus) sind alle Zahlen
darstellbar (auch negative, gebrochene, reelle ...). Auch eine
normale oder verkürzte Exponentialdarstellung (wie in der EDV) ist möglich.
Kleinstmögliche Basis
Bei normalen Zahlensystemen ist die kleinste Basis 2, bei Plus-Systemen 1:
Beim 1+ System haben alle Stellen den Wert 1 (vorm Komma: 1n = 1 ,
hinterm Komma: 1-n = 1 / 1n = 1 ).
Das 1+ System ist also nicht verkürzend, sondern eine Zahl
besteht aus ebensovielen Ziffern 1, wie der Zahlenwert beträgt.
Ein evtl. vorhandenes Komma hat keine Bedeutung.
Man könnte das 1+ System ein entartetes Stellenwertsystem nennen.
Trotzdem funktionieren die üblichen Algorithmen für Addition,
Multiplikation etc. auch hier. Sie sind aber umständlicher als nötig.
Z.B. kann der Additionsalgorithmus mit Übertrag ersetzt
werden durch das Verketten zweier Zahlen. Siehe den Artikel
über Figuren-Rechnen
Vergleich der Zahlenlängen
Die folgende Tabelle vergleicht die höchsten Zahlen, die mit
1 - 4 Ziffern dargestellt werden können, in einigen Zahlensystemen:
dem 2 und 2+ System, dem 3 und 3+ System, dem 10 und 10+ System.
(In Klammern: derselbe Zahlenwert im Dezimalsystem)
2 2+ 3 3+ 10 10+
-------------------- --------------------- -------------------
1 (1) 2 (2) 2 (2) 3 (3) 9 X (10)
11 (3) 22 (6) 22 (8) 33 (12) 99 XX (110)
111 (7) 222 (14) 222 (26) 333 (39) 999 XXX (1110)
1111 (15) 2222 (30) 2222 (80) 3333 (120) 9999 XXXX (11110)
-------------------- --------------------- ------------------
+ 100% + 50% + 11%
+ 1/1 + 1/2 + 1/9
Im Plus-System können mit gleichviel Stellen mehr Zahlen
dargestellt werden (aber weniger als im normalen Zahlensystem
mit um 1 höherer Basis). Je kleiner die Basis des Zahlensystems,
desto größer der Unterschied. Im Plus-System ist das b/(b-1) fache
an Zahlen darstellbar (b=Basis), also gerade der Quotient der
2 jeweils höchsten Ziffern. Dieses Verhältnis ändert sich
nicht mit der Basis oder der Zahlenlänge.
Kippen der Zahlendarstellung
Sowohl in Plus-Systemen wie in normalen Zahlensystemen gibt es
das Phänomen, dass die Zahlendarstellung bei Änderung des Werts um 1
plötzlich kippt, z.B. von 999 zu 1000 im Dezimalsystem.
Bei Plus-Systemen liegt dieser Übergang nicht bei den Potenzen
der Basis (auch nicht bei gebrochenen Zahlen, siehe unten):
im 10+System z.B. von XXX (=dezimal 1110) zu 1111 ,
allgemein von bbb (= 1110 im Nicht-Plus Zahlensystem) zu 1111
(Wert in beiden Systemen gleich).
Das kann man einerseits als Nachteil empfinden: Bei Nichtplus-
Systemen ist jede runde Zahl die kleinste Zahl ihrer Länge,
jede andere gleichlange Zahl ist größer.
Es ist somit einfach, die runden Zahlen anzugeben, zwischen denen
eine Zahl liegt: Im Zehnersystem liegt 567 zwischen 100 und 1000.
Im 10+ System liegt 567 zwischen den Zehnerpotenzen 9X und 99X,
was eigentlich genauso leicht erkennbar ist.
Rechnerisch ist es ein Vorteil: Bei den Rechenaufgaben 1000 + 1
und 1000 -1 kippt im üblichen Zehnersystem beim zweiten Ergebnis 999
die Darstellung völlig, was für Rechenanfänger schwierig ist.
(Erst durch die Macht der Gewohnheit, nach langer Übung,
erscheint das einfach).
Im 10+System sehen die entsprechenden Rechnungen so aus:
99X + 1 = 9X1 und 99X - 1 = 999. Das heißt, in Plus-Zahlensystemen
ändert sich bei der Subtraktion 'runde Zahl - kleine Zahl' die
Zahlendarstellung kaum.
Zahlenumwandlung
Die Zahlenumwandlung zwischen "normalem" Zahlensystem und Plus-
Zahlensystem mit gleicher Basis ist einfach:
Es unterscheiden sich nur die Zahlen, welche im im normalen
System die Ziffer 0 enthalten. Das sind genau die Zahlen,
welche im Plus-System die Ziffer b (= Basis) enthalten.
Man muß also jede Ziffer 0 in Ziffer b umwandeln bzw. umgekehrt,
wobei immer die nächsthöhere Ziffer um 1 geändert wird.
"normale" Zahl wird Plus-Zahl:
(Man streicht zuerst führende Nullen)
Man ersetzt jede Ziffer 0 durch b und subtrahiert dafür 1 von der
nächsthöheren Stelle.
(Der Zahlenwert bleibt gleich, weil diese 1 wegen des b-fachen Stellenwerts
soviel wert ist wie die Ziffer b an der nächstniederen Stelle).
Beispiele im Zehnersystem: 10 wird durch Ersetzen der 0 zu 1X und durch
Subtrahieren einer 1 von der linken Stelle zu X . 100 wird über 1X0, X0, XX zu 9x
Plus-Zahl wird "normale" Zahl:
Man ersetzt jede Ziffer b durch 0 und addiert dafür 1 zur
nächsthöheren Stelle.
(Der Zahlenwert bleibt gleich, weil diese 1 wegen des b-fachen Stellenwerts
soviel wert ist wie die Ziffer b an der nächstniederen Stelle).
Beispiele im Zehnersystem:
X wird durch Ersetzen zu 0 und durch Addieren von 1 zur nächsthöheren Stelle zu 10.
XX wird über 0X, 10X, 100 zu 110
Das Verfahren kan man in beiden Richtungen vereinfachen, indem man blockweise arbeitet:
Man ersetzt jede Folge ...000 durch ...99X und subtrahiert 1 von der Ziffer links von der Folge.
Bzw. man ersetzt jede Folge ...XXX durch ...110 und addiert 1 zur Stelle links von der Folge.
Die Umwandlung zwischen Plus-Zahlensystem und "normalem" Zahlensystem mit ungleicher Basis erfolgt ähnlich wie die Umwandlung zwischen 2 normalen Zahlensystemen mit ungleicher Basis:
3+ Zahl wird Zehnerzahl:
Die Umwandlung einer Zahl z.B. im 3+ System in eine Zehnerzahl
(allgemein: in ein Zahlensystem mit höherer Basis) ist einfach:
Man rechnet einfach im Dezimalsystem den Zahlenwert aus, d.h.
man multipliziert jede Ziffer mit ihrem Stellenwert und summiert
die Ergebnisse.
Zehnerzahl wird 3+ Zahl:
Die Umwandlung einer Zehnerzahl ins 3+ System (allgemein: in ein
Zahlensystem mit niedrigerer Basis) ist dagegen schwieriger:
Man rechnet zunächst die Zehnerzahl ins "normale" Dreiersystem
um mit folgendem bekannten Algorithmus zur Zahlenkonvertierung:
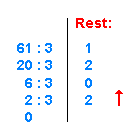
| Zehnerzahl 61 ins 3er-System umwandeln: - man dividiert 61 durch 3 - schreibt den Rest 1 schreibt daneben - schreibt das Ergebnis 20 darunter - verfährt entsprechend mit 20, usw. Die Reste, v.u.n.o. gelesen, ergeben die Dreierzahl 2021 |

Rechnen in Plus-Zahlensystemen
- Diese Teilbarkeitsregel ist schöner: Eine Zahl ist ohne Rest
durch die Basis b des Zahlensystems teilbar, wenn ihre letzte Ziffer = b ist.
Allgemein: Ist die letzte Ziffer ein Teiler der Basis des Zahlensystems,
oder enthält sie einen, so ist die ganze Zahl durch diese Teiler teilbar.
(Diese Regel gilt in normalen Zahlensystemen auch, aber nicht für Endziffer 0).
Die bekannten Teilbarkeitsregeln bzgl. mehrerer Endziffern gelten entsprechend,
die Teilbarkeitsregeln mit Quersumme, alternierende Quersumme genauso wie in
üblichen Zahlensystemen.
- Diese Teilbarkeitsregel ist schöner:
Eine Zahl ist ohne Rest durch bn teilbar, wenn sie
mit der Zahl bn endet.
(Im normalen Zahlensystem: ... wenn sie mit n Nullen endet)
- Die Folge der Potenzen der Basis ist vergleichbar regelmäßig:
(die optische Eleganz einer Zahlenfolge hängt auch von den Ziffernsymbolen ab!)
3er System: 1, 10, 100, 1000, 10000 entspricht 1, 3, 9, 27, 81
3+ System: 1, 3, 23, 223, 2223 entspricht 1, 3, 9, 27, 81
10+ System: 1, X, 9X, 99X, 999X entspricht 1, 10, 100, 1000, 10000
+ System: 1, b, ab, aab, aaab entspricht 1, b, b2, b3, b4
(a = zweithöchste Ziffer, b = höchste Ziffer = Basis)
Im 3+System wird zum vorigen Wert jeweils das 2-fache hinzu addiert.
Allgemein wird zum vorigen Wert jeweils das (b-1)-fache addiert.
- Will man eine runde Zahl vergrößern,
so muß man nur vorne Ziffern b-1 anfügen. Man braucht die
bestehende Zahl nicht zu ändern, im Ggs. zu normalen
Zahlensystemen, wo aus der bisher führenden 1 eine 0 wird.
- Der Stellenwert jeder Stelle ist bei runden Zahlen direkt ablesbar:
Er ist gleich dem rechten Zahlenteil bis zu dieser Ziffer (excl.).
Beispiel im 10+ System:
In der Zahl 999X (dez. 10 000) ist der Stellenwert der 2. Stelle von rechts = X (dez. 10),
der 3. Stelle von rechts = 9X (dez. 100), der 4. Stelle von rechts = 99X (dez. 1000).
Ausnahme: Der Stellenwert der Ziffer ganz rechts ist 1, der Gesamtwert
dieser Stelle also gleich der Ziffer.
- Generell gilt: die Ziffernfolge 99X beispielsweise ist
(egal ob als Zahl, am Zahlenende oder innerhalb der Zahl)
soviel wert wie eine 1 an der nächsthöheren Stelle.
Entsprechendes gilt z.B. für die Ziffernfolge 9X in 9X9X (dezimal 10100).
(Das gilt auch für Nachkommastellen, siehe unten)
- Das Einmaleins wird schwieriger: Die leicht rechenbaren Kombinationen
0 + n, 0 * n kommen bei
ziffernweiser Berechnung nicht vor, weil Zahlen nie die Ziffer 0 enthalten.
Stattdessen treten im Additions- und Multiplikationsalgorithmus die Kombinationen
b + n, b * n auf (b = Basis, n = eine Ziffer).
- Addition: funktioniert ähnlich wie bei üblichen Zahlensystemen:
ziffernweise Addition, beim kleinsten Stellenwert beginnend. Ist die Summe
von 2 Ziffern größer (nicht gleich) der Basis b, so wird sie um b erniedrigt
und es erfolgt ein Übertrag von 1 in die nächsthöhere Stelle. Beispiele:
b + 1 = 11, b + b = 1b im 3+ System: 1+1 = 2, 2+1 = 3, 3+1 = 11, 3+3 = 13, 3+3+1 = 21Das letzte Beispiel zeigt: auch bei der Addition von nur 2 Zahlen kann ein Übertrag 2 vorkommen, wenn 2 mal die höchste Ziffer und ein Übertrag aus der nächstniederen Stelle addiert werden.
- Addition-Sonderfall: runde Zahl + Zahl:
Die nichtrunde Zahl überlagert rechtsbündig die runde Zahl.
Links von der kürzeren Zahl wird ein Übertrag 1 addiert.Beispiele im 10+ System: 9999X 999X 99X 9X X + 345 + 345 + 345 + 345 + 345 ------- ------ ------ ------ ------ 9X345 X345 1345 445 355 Beispiele allgemein: aaaab aaab aab ab b + xyz + xyz + xyz + xyz + xyz ------- ------ ------ --------- --------- abxyz bxyz 1xyz (x+1)yz x(y+1)zBeweise: Man führe die allgemeinen Rechnungen aaaab + xyz ... durch.
Wenn die runde Zahl länger ist als die andere, läßt sich das Additionsverfahren besonders einfach formulieren:
Man hängt die nichtrunde Zahl rechts an die runde Zahl an und streicht links genausoviele Ziffern. (siehe die jeweils ersten 2 Beispiele oben)
- Subtraktion: funktioniert ähnlich wie bei üblichen Zahlensystemen:
ziffernweise Subtraktion, beim kleinsten Stellenwert beginnend. Sind 2 Ziffern gleich, muß man, um 0 als Differenz und Ergebnisziffer zu vermeiden, von der nächsthöheren Stelle eine 1 "borgen", die an der niederen Stelle zur Ziffer b (= Basis) wird.
Das bekannte Verfahren, die Subtraktion durch Addition des Komplements zu ersetzen (im Zehnersystem des Neunerkomplements, danach Rücktrag der höchsten Ziffer 1 in die niederste Stelle), funktioniert bei Plus-Systemen genauso, solange nur der Subtrahend nicht die Ziffern b oder b-1 enthält (b=Basis). Andernfalls kann das entsprechende Komplement nicht gebildet werden. Dies ist nachteilig, da dieses Verfahren bei elektrischen und mechanischen Rechnern oft benutzt wird.
- Multiplikation: funktioniert ähnlich wie bei den üblichen Zahlensystemen, mit Übertragsbildung ähnlich wie bereits bei der Addition beschrieben
- Multiplikation-Sonderfall: Zahl * runde Zahl
Eine runde Zahl bn hat im Plus-System die Darstellung ...aaab (b = Basis, a = Basis-1)
Sie wird mit einer beliebigen Zahl xyz multipliziert, indem man die Zahl xyz-1 voranstellt
Beispiel im 10+ System: 123 * 999X = 122999X (also 122 * 999X + 999X)
Beispiel allgemein: ab * ab = aaab
Beweis: Man führe die allgemeine Rechnung aaab * xyz durch. Oder:
Die runde Zahl aaab ist sozusagen der Stellenwert der vorangestellten Zahl xyz-1 . Der Wert der ganzen Zahl ist also (xyz-1) * aaab + aaab
- Multiplikation-Sonderfall: Ziffer * runde Zahl
Eine runde Zahl wird mit einer Ziffer z multipliziert, indem man die Ziffer 'z-1' voranstellt
Beispiel im 10+ System: 5 * 999X = 4999X (also 4 * 999X + 999X)
Diese Regel ist nur ein Spezialfall obiger Regel, wobei die nichtrunde Zahl eben nur aus 1 Ziffer besteht. Die Regel gilt auch für z=1: z-1 ergibt nichts
- Umgekehrt läßt sich eine runde Zahl mit mindestens 2 Stellen, und jede Zahl, die durch b2 teilbar ist (sie endet immer mit den Ziffern b-1,b), durch b dividieren, indem man die vorletzte Ziffer b-1 streicht.
- Multiplikation-Sonderfall: Ziffer z * Zahl 111... (beliebig viele Einsen)
Ergibt wie im normalen Zahlensystem zzz. Im Plus-System mit Basis b läßt sich auch der Fall 111 * b = bbb so einfach rechnen, auch der Fall ttt * (b/t) = bbb, wobei b= Basis, t=Teiler der Basis: z.B. gilt im 10+ System 222 * 5 = XXX (X = Ziffer 10). Diese Multiplikationen sind bei Strichziffern besonders anschaulich.
- Multiplikation-Sonderfall: Zahl * b (=Basis)
Läßt sich natürlich nach dem allgemeinen Multiplikationsalgorithmus (stellenweise Multipl.) berechnen, oder einfacher nach obiger Methode 'Zahl mal runde Zahl', also: an Zahl-1 die Ziffer b anhängen
- Multiplikation-Sonderfall: Ziffer mal b (=Basis)
Geht am besten nach obiger Methode für "Zahl mal b": Man subtrahiert 1 von der Ziffer und fügt unten die Ziffer b an. Anders formuliert: Man stellt die Ziffer über die Ziffer b und nimmt oben 1 Hölzchen weg. Bei Zahlendarstellung durch Strichziffern (siehe Artikel über das Vierersystem) kann man die Regel noch anders formulieren, sehr anschaulich: Man fügt zur Ziffer rechts b-1 Striche / Hölzchen hinzu und überträgt alle Hölzchen, die über die Basiszahl b hinausgehen, nach oben in die nächsthöhere Stelle:
- Multiplikation-Sonderfall: Zahl * b + b (= Basis)
Man hängt einfach die Ziffer b an die Zahl an! In normalen Zahlensystemen ist das nicht möglich, weil es die Ziffer b nicht gibt.
Einfach zu rechnen ist auch der allgemeine Fall (Zahl * bn ) + bn + bn-1 ... + b1: man hängt n-mal die Ziffer b an die Zahl an.
In Plus- und Nicht-Plus Zahlensystemen einfach zu rechnen ist der Fall (Zahl * bn ) + bn-1 + bn-2 ... + b0: man hängt n mal die Ziffer 1 an die Zahl an.
Im 3+ System gibt es einen besonders einfachen Multiplikationsalgorithmus:
Man wandelt zu multiplizierende Zahlen um vom 3+ System ins 3+1 System, indem man 1 subtrahiert und eine Anfangs1 hinzufügt. Nun berechnet man ihr Produkt nach dem einfachen Multiplikationsalgorithmus des 3+1 Systems. Das Ergebnis verwandelt man zurück in eine Zahl des 3+ Systems, indem man die Anfangs1 streicht und 1 addiert.
Man kann auch obigen Algorithmus, leicht geändert, direkt im 3+ System verwenden:
1) Man subtrahiert von beiden Zahlen je 1 und verkettet die neuen Zahlen. Dann subtrahiert [addiert] man dort, wo die hintere Zahl Ziffer 1 [3] hat, jeweils stellenrichtig die vordere Zahl. Zum Ergebnis addiert man 1
2) Oder: Man verkettet beide Zahlen. Man subtrahiert davon beide Zahlen (die hintere einfach, indem man diese Zahl in der Verkettung streicht). Dann subtrahiert [addiert] man dort, wo die hintere Zahl (vor Streichung) Ziffer 1 [3] hatte, jeweils stellenrichtig die vordere Zahl.
- Division: Geht ähnlich wie bei den üblichen Zahlensystemen. Eine ganzzahlige Division ohne Rest geht praktisch genauso.
Dividiert man eine runde Zahl durch eine runde Zahl, so fallen nur vorne Ziffern weg. Bei normalen Zahlensystemen dagegen fallen hinten Ziffern weg, weshalb man dann ggf. die Zahl nach rechts verschieben muß, um stellenrichtig weiterarbeiten zu können. Beispiel im 10er und im 10+ System:10000 : 100 = 100 999X : 9X = 9XGeht eine ganzzahlige Division nicht auf, so hängt man, wenn der Rest kleiner ist als der Divisor, an den Rest die Ziffer b (=Basis) an (im Beispiel die Ziffer X des 10+Systems, rot). Entsprechend muß man an der vorigen Stelle des Rests eine 1 subtrahieren. Dieses Verfahren ist also umständlicher als beim normalen Zahlensystem (einfach 0 anhängen). Beispiel:
1111 : 9X = 11,11 (entspricht 1111 : 100 = 11,11) -9X --- 111 -9X --- 11 XX -9X --- X 9X -9X --- 0
- Verketten von 2 Zahlen = kombinierte Addition / Multiplikation:
Beispiel: Verkettung von 123 mit 4567 = 1234567
Bedeutung im üblichen 10er-System: 123*104 + 4567, wobei 4 = Länge der angehängten Zahl 4567.
Bedeutung im 10+ System: dieselbe, auch wenn Zahlen die Ziffer X enthalten. Denn die Stellenwerte sind ja dieselben.
Gebrochene Zahlen
Wie in üblichen Zahlensystemen wird ein Dezimalkomma verwendet, oder einfacher die Ziffer 0, die sonst nur allein vorkommt als Zahl 0
(Zur besseren Verständlichkeit für Ungeübte benutzen wir im folgenden ein Komma)
Eine gebrochene Zahl darf mit Dezimalkomma beginnen. Beispiel: ,123
Der Stellenwert der n-ten Stelle nach dem Komma ist wie bei den üblichen Zahlensystemen b-n := 1 / bn (b=Basis)
Beispiel: 1,123 bedeutet im Zehn- und 10+ System dasselbe, nämlich:
1 + 1*10-1 + 2*10-2 + 3*10-3 = 1 + 1/10 +2/100 + 3/1000 = 1 + 123 / 1000
Eine Verschiebung des Kommas um 1 Stelle nach rechts / links bewirkt eine Multiplikation / Division der Zahl mit der Basis. Beispiele:Zahlensystem: 10 10+ ------------- ------------- ------------ 1000 = 1000 99X = 99X 100,0 = 100 99,X = 9X 10,00 = 10 9,9X = X 1,000 = 1 ,99X = 1In Plus- und Nichtplus-Zahlensystemen können runde Zahlen nach einer Links-Kommaverschiebung verkürzt werden, beispielsweise 10,00 zu 10 und 9,9X zu X
Wie schon weiter vorne erwähnt, ist eine Ziffernfolge der Art ..99X (allgemein der Art ..aab, a = Basis-1, b = Basis) immer soviel wert wie eine 1 an der nächsthöheren Stelle. Das gilt auch, wenn die Ziffernfolge nach dem Komma steht oder ein Komma enthält. Die Ziffernfolgen ,X und ,9X und ,99X in obiger Tabelle sind also jeweils 1 wert. Die Ziffernfolge 9,9X ist also 10 wert (= Stellenwert der 2. Stelle vor dem Komma)
In Plus-Zahlensystemen kann also der Nachkommateil den Wert 1 erreichen oder übersteigen, siehe Tabelle. Anderes Beispiel: ,XX = 10/10 + 10/100 = 1,1
Jede gebrochene Zahl größergleich 1/b ist mit 1 Komma darstellbar.
Kleinere Zahlenwerte benötigen mehrere Kommas (oder den Summand -1):Zahlensystem: 10 10+ 10+ ------------- ---------- --------- ---------- 0,1 ,1 ,1 0,01 ,,1 ,X1 -1 0,001 ,,,1 ,9X1 -1 0,0001 ,,,,1 ,99X1 -1 0,0003 ,,,,3 ,99X3 -1Hinter dem 1. Komma dürfen weitere folgen, um Leerstellen anzuzeigen. Das Komma kann nur einmal oder als Block auftreten, aber nicht zwischen Nachkommaziffern eingestreut! Denn Nachkommaziffern mit zwischenliegender Null lassen sich immer in die Plus-Darstellung ohne Null überführen. Beispiel:
0,10310 wird zu 0,X310+ (denn 10310 = X310+)
Steht vor einem Kommablock mindestens 1, läßt sich eine solche Zahl mit nur 1 Komma schreiben: Man subtrahiert 1 vom Vorkommateil und schlägt diese 1 dem Nachkommateil zu. Beispiel: 1,01 wird im 10+ System zu 1,,1, was sich auch als ,X1 darstellen läßt. (Ob das sinnvoll ist, ist die andere Frage).
Auch wenn vor einem Kommablock nichts steht, läßt sich eine solche Zahl mit nur 1 Komma schreiben: man addiert 1, wandelt um in Darstellung mit 1 Komma und fügt den Ausdruck -1 hinzu. Beispiel: 0,01 wird zu 1,01 - 1 und im 10+ System zu ,X1 - 1 (Tabelle oben rechts)
Man könnte deshalb statt der Ziffer 0 auch die Ziffer -1 einführen und sie als Dezimalkomma verwenden. (Die Zahl Null wird dann ausgedrückt als Ziffernfolge 1-1). Die Ziffer -1 wird als Dezimalkomma verwendet, und deshalb wird zum Nachkommateil als Ausgleich 1 addiert. Dann ist jeder Nachkommateil größer 1 und deshalb jede gebrochene Zahl mit nur 1 Komma darstellbar.
Manche gebrochenen Zahlen haben also im Plus-System mehrere mögliche Darstellungen. (Vergleiche die unendlich vielen Darstellungen 0,1 0,10 0,100 ... in normalen Zahlensystemen!). Folgende Zahldarstellungen sind kürzbar (vergleichbar dem Kürzen von Brüchen) und sollten in die kürzestmögliche Form umgewandelt werden:
- Wenn die letzte Nachkommaziffer b ist: ,99X = ,9X = ,X = 1 Anderes Beispiel: 1,3b = 1,4 . Die Ziffer X (allgemein:Ziffer b = Basis) ist soviel wert wie eine zur vorigen Stelle addierte 1
- Wenn die erste Nachkommaziffer b ist: Beispiel: Die Zahl 1,b3 ist gleich 2,,3 (Es ergibt sich immer ein Kommablock, außer wenn die Zahl nur 1 Nachkommaziffer hatte).
Es ist oft besser, statt gebrochener Zahlen eine verkürzte Exponentialdarstellung wie in der EDV zu verwenden, z.B. 123 e 55 ( Kurzform für 123 * 1055, e = Kürzel für 'Exponent' )
Was sind runde Zahlen?
Allgemein gelten die Potenzen der Basis eines Zahlensystems als runde Zahlen. Sie haben in üblichen Zahlensystemen die Form 10, 100, 1000 ... , in Plus-Systemen die Form b, ab, aab, aaab (b = Basis = höchste Ziffer, a = zweithöchste Ziffer). Hier ist jeweils die nächste Zahl das b-fache der vorigen. Diese runden Zahlen können in beiden Arten von Zahlensystemen einfach mit einer anderen Zahl multipliziert werden.
Intuitiv würde man eher eine Folge gleicher Ziffern als runde Zahl ansehen. Kann man ein Zahlensystem so gestalten, daß diese optisch runden Zahlen auch mathematisch rund sind?
Das ist in Plus- und Nicht-Plus-Systemen diskussionswürdig: In üblichen Zahlensystemen könnte man vorzugsweise die Zahlen 1, 11, 111 ... als rund definieren (und z.B. Maßsysteme danach ausrichten), in Plus-Systemen vorzugsweise die Zahlen 1, 11, 111 ... oder b, bb, bbb ... . Hier ist jeweils die nächste Zahl gleich 'vorige Zahl + eine Potenz der Basis'. Diese 2 Arten von runden Zahlen können einfach mit b multipliziert werden. Die Multiplikation mit einer beliebigen Ziffer (nicht Zahl) ist bei den Zahlen 1, 11, 111 ... einfacher. Bei 111... ist der Zahlenwert einfach die Summe der Stellenwerte. Bei bbb... ist der Zahlenwert gleich dem Wert der endlichen Reihe b + b*b + b*b*b + ...
Die erste Art von runden Zahlen (Potenzen der Basis) wirkt etwas technischer, während die zweite Art von runden Zahlen (Summe der Potenzen der Basis) etwas organischer, komplizierter wirkt. Letztere erinnern an Strukturen bei Verwaltung, Militär etc., wo eine 'Einheit' nicht nur aus b Untereinheiten besteht, sondern auf der neuen Ebene noch zusätzliches Personal etc. benötigt. Die zweite Art von runden Zahlen könnte für Potenzreihen, Polynome, Fraktale, selbst grundlegende zahlentheoretische Berechnungen wie Primzahlen vorteilhaft sein. Interessant ist die Frage, ob runde Zahlen der Form bbb.. , die nur in Plus-Systemen möglich sind, irgendeinen Vorteil bieten.
Bewertung der Plus-Systeme
- Die anfangs genannten 5 Verbesserungswünsche sind erfüllt:
Ziffern 1 bis b; in Zahlen keine Formulierung 0*bn; nur 1 Darstellungsmöglichkeit pro Zahl (leider nur bei ganzen Zahlen); Basis runder Zahlen erkennbar; Wert runder Zahlen und "größter" Zahlen (nur Ziffern b) rein aus den sichtbaren Ziffern berechenbar
- Man kann bei gleicher Stellenzahl größere Zahlenwerte darstellen.
Man braucht in einem Plus-System nicht mehr Ziffern als im entsprechenden Nicht-Plus-System, da man die Zahl Null z.B. durch 1 oder 2 Dezimalkommas darstellen kann.
- Zahlendarstellung durch Strichziffern: Strichziffern bis zu 4 parallelen Strichen lassen sich durch die Finger einer Hand leicht darstellen. Strichziffern bis zu 3 parallelen Strichen III sind leicht erkennbar, bei mehr IIII muß man genauer hinschauen.
Bei Basis 2 und 3 sind also bzgl. der Strichdarstellung die Plus-Systeme vorteilhafter: Die maximale Ziffer ist 1 höher (2 statt 1 bzw. 3 statt 2). D.h. die menschliche Fähigkeit, Bündel bis zu 3 Strichen gut unterscheiden zu können, ist besser ausgenutzt. Umgekehrt sind ab Basis 4 die üblichen Zahlensysteme vorteilhafter, weil hier die größte Ziffer um 1 kleiner ist und damit als Strichziffer besser erkennbar.Bei Plus-Zahlensystemen enthalten alle Zahldarstellungen durch Strichziffern (außer Null) nur senkrechte Striche. Das macht die Darstellung einheitlich, aber u.U. weniger markant und schlechter lesbar. Bei "normalen" Zahlensystemen kommt auch 0 als Kringel (oder schräger oder waagrechter Strich) vor.
Will man die Ziffern einer Zahl als Perlen darstellen (siehe Figuren-Rechnen), so ergibt bei Zahlen "normaler" Zahlensysteme die Ziffer 0 eine Lücke, die Zahldarstellung ist zerissen, während bei Plus-Systemen jede Ziffer durch mindestens 1 Perle repräsentiert wird und die Zahldarstellung zusammenhängend bleibt. Das zeigt folgendes Beispiel im 4er-System (130234 = 124234+):
Beim Kugelrechner, einer mechanischen Rechenmaschine mit rollenden Kugeln, ist das Fehlen der Ziffer 0 nützlich: Jede Ziffer wird durch die entsprechende Anzahl Kugeln dargestellt, aber mindestens eine. (Rechnungen mit der Zahl 0 kann man auch ohne Gerät durchführen)
Dadurch bleibt die Zahl optisch zusammenhängend, und auch technisch: Bei der sukzessiven Abarbeitung (z.B. Addition) von Ziffern mit gleichem Stellenwert ist es (je nach Schaltmechanismus) nötig, daß pro Stelle mindestens 1 Kugel rollt, die den Schaltvorgang der nächsten Stelle auslöst. (Es ist aber auch ein Schieber-ähnlicher Mechanismus denkbar, der den Schaltvorgang jeder Stelle mit einer gewissen Verzögerung automatisch auslöst).
Bei linearer Anordnung aller Perlen kann man die Ziffern durch je 1 Trennzeichen trennen, oder (bei Plus-Zahldarstellung) für die erste Perle jeder Ziffer eine besondere Perle verwenden, was Platz spart. Das erspart ein Trennzeichen nach jeder Ziffer. Das könnte in biologischen Systemen nützlich sein (Gencode: anderes Protein für erste Perle?)
- Die Potenzen der Basis haben eine ähnlich regelmäßige Darstellung in beiden Arten von Zahlensystemen.
- Die Addition 'runde Zahl + Zahl' ist ähnlich einfach in beiden Arten von Zahlensystemen.
- Bei "normalen" Systemen kann man eine Zahl einfach mit einer runden Zahl (z.B. 100) multiplizieren durch Anhängen von Nullen: d.h. man streicht an der runden Zahl die führende 1 und hängt den Rest (die Nullen) an die andere Zahl.
Bei Plus-Systemen ist dieser Fall vergleichbar einfach: man muß zwar erst 1 subtrahieren, d.h. die Zahl um 1 herunterzählen, kann dann aber die runde Zahl als Ganzes anhängen.
- Bei Plus-Systemen kann auch der Fall (Zahl * b) + b einfach gerechnet werden, auch der allgemeine Fall (Zahl * bn ) + bn + bn-1 ... + b1: man hängt einfach n-mal die Ziffer b an die Zahl an.
- Bäume: Eine Zahl des Typs 111... gibt in in beiden Arten von Zahlensystemen die Knotenzahl eines Baums mit 1 Wurzelknoten, jeweils b Nachfolgern pro Knoten und n Ebenen (n = Anzahl der Einsen) an.
Aber: Numeriert man die Nachfolgeknoten mit Ziffern, so ergibt sich im +System die natürliche Numerierung 1 bis b (=Basis), im normalen Zahlensystem die Numerierung 0 bis b-1. Die Numerierung eines Abzweigs mit 0 ist aber unnatürlich und problematisch: wenn man eine Zahl als Pfad im Baum auffaßt (Ziffer = Nummer des Nachfolgeknotens) bzw. als Adresse eines Knotens, so können verschiedene Pfade / Adressen, z.B. 10 und 010, den gleichen Zahlenwert haben, was ungünstig ist, wenn man eine Adresse als Zahl abspeichern will. Und technisch wird z.B. ein Pfad 010 in einem Feld mit 8 Ziffern als 0000 0010 abgespeichert, was den Pfad verfälscht.
Aus diesen Gründen ist ein Plus-System für die Zahlendarstellung eines Baumes vorteilhafter (z.B. das 2+ System für Binärbäume).
- Bei Bankkonten, Telefonnummern, allgemein bei Nummerierung in Entscheidungsbäumen ist das Fehlen der 0 günstig: Es besteht keine Verwechslungsgefahr bei Weglassen der 0 (gleicher Zahlenwert bei gleicher Zeichenkette)
- Bei Geldscheinen und anderen Dingen, selbst physikalischen Maßsystemen, wäre es wohl egal, ob die nächstgrößere Einheit genau das b-fache der vorigen ist. Hier könnte man sich auch an eine Darstellung runde Zahl = bbb gewöhnen, wie an einen logarithmischen Maßstab. Solche Zahlen bbb.. (b=Basis) sind nur in Plus-Systemen möglich, aber vermutlich unzweckmäßiger.
- Lassen sich Wurzel 2, Pi, e ... in einem Plus-System einfacher darstellen?
- Sowohl in Plus-Systemen wie in normalen Zahlensystemen gibt es das Phänomen, dass die Zahlendarstellung bei Änderung des Werts um 1 plötzlich kippt, z.B. von 999 zu 1000 im Dezimalsystem. Bei Plus-Systemen liegt dieser Übergang nicht bei den Potenzen der Basis, sondern höher, was die Subtraktion 'runde Zahl - kleine Zahl' erleichtert.
Einen gleitenden Übergang erzielt man mit den bekannten Gray Codes, die zwar auch eine Art Stellenwertsystem haben, aber sonst zur Bildung eines Zahlensystems für den menschlichen Gebrauch eher ungeeignet erscheinen. Diese Frage sollte man aber im Auge behalten.
- Beim Vergleich von üblichen Zahlensystemen und Plus-Systemen muß man sich klarmachen: Auch die üblichen Systeme haben viele kleine Ungeschicklichkeiten, die durch jahre- oder jahrzehntelange Übung nicht mehr auffallen. Z.B. das obenerwähnte Kippen der Zahlendarstellung beim Übergang von 99 zu 100 - keine Ziffer bleibt gleich! Oder die anfangs erwähnten Nachteile.
Fazit: Plus-Zahlensysteme sind durchaus praktikabel, vergleichbar den üblichen Zahlensystemen. Eine Verbesserung sind vielleicht die Plus1- Zahlensysteme, z.B. das 3+1 Zahlensystem
Vorteilhaft sind Plus-Systeme bei Iris-Koordinaten, einem speziellen Koordinatensystem. Auch für Sonderzwecke wie Baumstrukturen, mechanische Rechner, spezielle Rechenverfahren oder Kryptographie (Verschlüsselung) könnten sie vorteilhafter sein.
Auf jeden Fall sind sie theoretisch interessant - auch weil sie die oft gelesene Behauptung widerlegen, für Stellenwertsysteme sei die Ziffer 0 nötig, und das kleinste Stellenwertsystem sei das Zweiersystem (in Wirklichkeit das 1+ System)
Die Plus-Systeme könnten historisch sein: z.B. als man in Europa das Dezimalsystem einführte, aber die Null noch nicht kannte, könnte man obige Algorithmen zur Addition einer runden Zahl und Multiplikation mit einer runden Zahl verwendet haben.
Die Benutzung der hier beschriebenen Techniken ist frei Stand: 15. 7. 2009 Autor und Erfinder: Leonhard Heinzmann Homepage