(Jede Zahl hoch Null ist per Definition =1).
Entsprechend ist im normalen Dreiersystem die Zahl 222 definiert als:

          222    =    2*9  +  2*3  +  2*1    =    2*32  +  2*31  + 2*30

Die Zahl 222 im Dreiersystem bedeutet also dasselbe wie die Zahl 26 im Dezimalsystem. 10 bzw. 3 nennt man die Basis des betreffenden Zahlensystems. Zur Unterscheidung schreibt man auch   222₁₀ bzw.   222₃

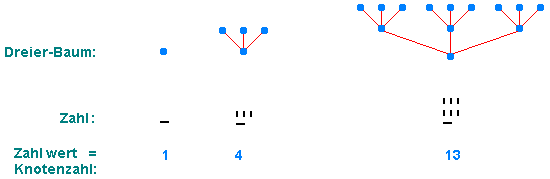
Das 3+1 Zahlensystem

ist ein Stellenwertsystem zur Basis 3. Gegenüber dem "normalen" 3-er System hat es folgende Besonderheiten (wir beschränken uns im Moment auf ganze Zahlen größer 0):

    - Es werden die  Ziffern  1 bis 3  verwendet   (nicht 0 bis 2)

    - Es gibt 2 Einerstellen:
       1) Jede Zahl endet mit 1, der Anfangs-Eins
           (so genannt, weil sie bei Strichziffern (s.u.) am Anfang steht)
       2) Dann folgt eine  normale Einerstelle,  die wie alle folgenden
           Stellen  Werte von 1 bis 3 annehmen kann.

    - Das Zählen erfolgt ähnlich wie bei "normalen" Zahlensystemen:
      Die aktuelle Stelle (Schale) wird bis zur höchsten erlaubten Ziffer
      (3, außer bei der Anfangs-1) hochgezählt.  Wird dieses Maximum
      überschritten,  wird die Stelle auf  1 (nicht 0)  zurückgesetzt,  und
      in die  nächsthöhere  Stelle  wird eine 1 übertragen.


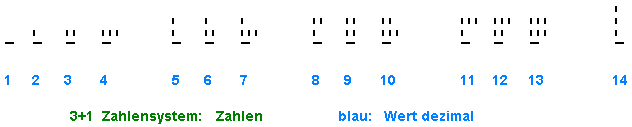
               Die ersten Zahlen im  10-er  und  3+1 System:

  10-er System  

   3+1 System

     1
     2
     3
     4

     5
     6
     7

     8
     9
    10

    11
    12
    13

    14
    15
    16
     .
     .

     1
    11                (1*1 + 1)
    21                (2*1 + 1)
    31                (3*1 + 1)

   111          (1*3 + 1*1 + 1)
   121          (1*3 + 2*1 + 1)
   131          (1*3 + 3*1 + 1)

   211          (2*3 + 1*1 + 1)
   221          (2*3 + 2*1 + 1)
   231          (2*3 + 3*1 + 1)

   311          (3*3 + 1*1 + 1)
   321          (3*3 + 2*1 + 1)
   331          (3*3 + 3*1 + 1)

  1111    (1*9 + 1*3 + 1*1 + 1)
  1121    (1*9 + 1*3 + 2*1 + 1)
  1131    (1*9 + 1*3 + 3*1 + 1)
     .
     .

In beiden Zahlensystemen sind alle Zahlen darstellbar. Und zwar eindeutig, d.h. es gibt keine 2 Darstellungsmöglichkeiten für dieselbe Zahl (abgesehen von führenden Nullen im Zehnersystem).

Strichziffern,     Multiplikation mit 3

Obige Zahlen des 3+1 Systems wirken umständlich. Übersichtlicher wirken sie (nach etwas Gewöhnung) bei Darstellung durch Strichziffern: Die Anfangs-1 ist ein waagrechter Strich, die Ziffern 1 bis 3 sind 1-3 senkrechte Striche nebeneinander:



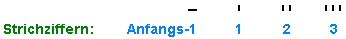
Die Schreibrichtung ist senkrecht von unten nach oben, der kleinste Stellenwert ist unten. Vorteile: Die Strichzifferdarstellung paßt zur Lautbildschrift, einer akustisch lesbaren Bilderschrift mit dieser Schreibrichtung. Auch sind bei nebeneinanderstehenden Zahlen dann Ziffern mit gleichem Stellenwert auf gleicher Höhe. Das erleichert Addition und Subtraktion, den Wertevergleich von Zahlen anhand ihrer Höhe (jede Zahl ist sozusagen ein Blockdiagramm; bei gleicher Höhe entscheidet zunächst die Breite der obersten Ziffer), u.Ä.:






Obige Strichziffern sind linksbündig. Möglicherweise sind zentrierte Strichziffern ergonomischer. Beispiele im Artikel über das Vierersystem

Markante Zahlenreihen:

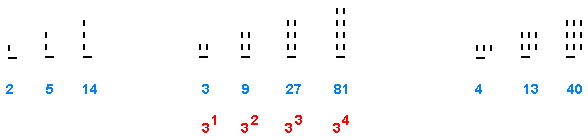
          - Hängt man an die Anfangs-1 laufend eine Ziffer 1 an, so gilt:
                    Zahl = Vorgängerzahl * 3  - 1

          - Hängt man an die Anfangs-1 laufend eine Ziffer 2 an, so gilt:
                    Zahl = Vorgängerzahl * 3
            Man erhält also gerade die Potenzen der Basis 3  (3,9,27..)

          - Hängt man an die Anfangs-1 laufend eine Ziffer 3 an, so gilt:
                    Zahl = Vorgängerzahl * 3  + 1

Im Zehnersystem wird eine Zahl mit der Basis 10 multipliziert, indem man eine 0 anhängt. Im 3+1 System wird eine Zahl mit der Basis 3 multipliziert, indem nach der Anfangs-1 eine 2 einschiebt. Siehe oben die Folge der Potenzen von 3. Weitere Beispiele:






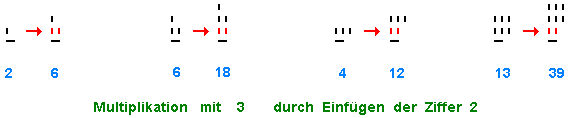
Obige Multiplikationsregel ist leicht zu beweisen: Alle Ziffern außer der Anfangs-1 werden durch das Einschieben der 2 auf die nächsthöhere Stelle gehoben, also mit 3 multipliziert. Die Anfangs-1 wird durch Anhängen der Ziffer 2 zur Zahl 3, also auch verdreifacht. Beweisende

Das heißt, man multipliziert eine Zahl mit 3, indem man aus der Anfangs-1 eine 3 macht, mit 9, indem man aus der Anfangs-1 eine 9 macht, mit 27 ... etc. (sukzessive Anwendung der Multiplikation mit 3).

Umgekehrt ausgedrückt: Man multipliziert eine Potenz der Basis mit einer beliebigen Zahl, indem man an die Potenz-Zahl oben diese Zahl anfügt (wobei deren Anfangs-1 weggelassen wird). Siehe unten den allgemeinen Multiplikationsalgorithmus, Sonderfälle.

Teilbarkeit und Division durch 3

Aus dem vorigen Abschnitt folgt sofort: Eine Zahl ist genau dann ohne Rest durch 3 teilbar, wenn sie mit 3 beginnt. Durch 9 teilbar, wenn sie mit 9 beginnt, durch 27, wenn sie mit 27 beginnt, etc. ...
(Denn nur Zahlen, die aus Multiplikation einer ganzen Zahl mit 3 entstehen können, sind durch 3 teilbar, etc.).
Die Division durch 3 geht umgekehrt wie die Multiplikation, d.h. man macht aus der 3 am Anfang eine 1, indem man nach der Anfangs-1 die Ziffer 2 entfernt. Entsprechend dividiert man durch 9, indem man aus der 9 am Anfang eine 1 macht, d.h. nach der Anfangs-1 zwei Ziffern 2 entfernt, durch 27 ... etc.


Auch die ganzzahlige Division von Zahlen, die nicht ohne Rest durch 3 teilbar sind, geht ähnlich einfach:
Entfernt man bei einer Zahl die erste Ziffer nach der Anfangs-1, so erhält man das gerundete Ergebnis von Zahl/3.
So werden 2,3,4 zu 1; und 5,6,7 zu 2; und 8,9,10 zu 3; und 11,12,13 zu 4, etc. War die entfernte Ziffer 1, so wurde aufgerundet, war sie 3, wurde abgerundet, war sie 2, wurde nicht gerundet. Will man das nicht gerundete ganzzahlige Ergebnis, dann muß man am obigen Ergebnis 1 subtrahieren, wenn Ziffer 1 entfernt wurde.

Entsprechend dividiert man eine Zahl ganzzahlig durch 9, indem man die 2 ersten Ziffern nach der Anfangs-1 entfernt, durch 27, indem drei Ziffern entfernt, etc.

Teilbarkeit durch 2:   Eine Zahl ist gerade, wenn ihre Quersumme gerade ist.
(Bei Strichzifferdarstellung ist die Quersumme gleich der Anzahl der Striche). Einfacher: Eine Zahl ist gerade, wenn die Anzahl ihrer ungeraden Ziffern gerade ist. Denn jede Addition einer ungeraden Ziffer zur Quersumme wechselt das Ergebnis, während es bei Addition der geraden Ziffer 2 gleichbleibt. Noch einfacher: Um die ungeraden Ziffern nicht zählen zu müssen, geht man sie durch und merkt sich nur das jeweilige Zwischenergebnis: ungerade - gerade - ungerade etc., oder zählt sie modulo 2: 1 - 2 - 1 etc.   (Schneller geht's, wenn man beim Zählen die Anfangs-1 wegläßt und mit "gerade" anfängt: gerade - ungerade ... bzw. 2 - 1 - 2).

Addition, Subtraktion

Beides funktioniert wie auch in anderen Zahlensystemen. Beide Einerziffern einer Zahl behandeln wir als 2 getrennte Ziffern (man könnte sie genausogut zusammen als 1 Ziffer behandeln).

Beispiel Addition: Man beginnt wie üblich bei der niederwertigsten Stelle, d.h. man addiert zuerst die beiden Anfangs-Einsen. Da diese Stelle keine größere Ziffer als 1 haben kann, bleibt nur eine Anfangs-1, die andere geht als Übertrag in die nächsthöhere Stelle. (Aus dem waagrechten wird dabei ein senkrechter Strich - kein Problem.) Diese Übertrags-1 ergibt mit den beiden Einsen der Zahlen 5 und 8 in der zweiten Einerstelle eine 3. Auch in der nächsthöheren Stelle ergeben 1 + 2 Striche zusammen 3.





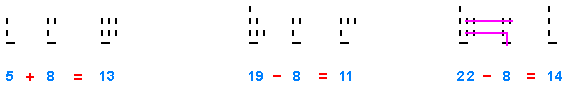
Beispiel Subtraktion 19 - 8 : Man subtrahiert zunächst die zweite Anfangs-Eins von der ersten, was Null ergibt. Da aber an dieser Stelle eine Anfangs-1 stehen muß, subtrahiert man 1 von der nächsthöheren Stelle, der zweiten Einerstelle.
(Normalerweise faßt man diese 2 Aktionen zusammen, indem man die Anfangs-1 der 2. Zahl von der zweiten Ziffer der 1. Zahl subtrahiert: Beide haben ja gleichen Stellenwert) Zieht man noch die entsprechende Ziffer 1 der zweiten Zahl ab, bleibt 1 an dieser Stelle. An der nächsthöheren Stelle ergibt 2 - 2 = 0. Da wir keine Null verwenden, holt man eine 1 von der nächsthöheren Stelle (die damit erlischt). Diese 1 wird zur 3, weil sie oben ja den 3-fachen Wert hatte.
Soll von einer Zahl eine größere subtrahiert werden, z.B. 8-19, so dreht man das Ganze um, also 19-8, rechnet und gibt dem Ergebnis 11 ein negatives Vorzeichen:   -11

Dank der Strichzifferdarstellung braucht man keine Additionstabelle (kleines Einsundeins) im Kopf zu haben. Man verschiebt einfach Striche (man könnte auch Hölzchen nehmen). Und bei Subtraktion (Beispiel 22 - 8, im Bild oben rechts) kann man nicht nur gleiche positive und negative Ziffern streichen, sondern auch bei ungleichen Ziffern gleichviele Striche. Manchmal hat man dann schon das Ergebnis.

Multiplikation

Der übliche Multiplikationsalgorithmus funktioniert auch hier (wenn man die 2 Einerstellen zusammenfaßt). Es gibt jedoch einen viel einfacheren Multiplikationsalgorithmus. Wir erklären ihn an einem Beispiel:





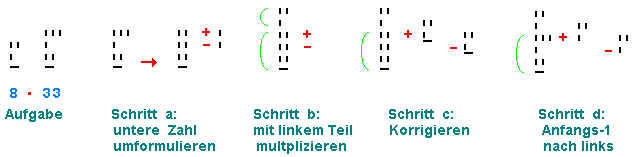
- Gegeben ist die Aufgabe 8*33

- Schritt 1: man stellt beide Zahlen einfach übereinander,
  läßt aber die Anfangs-1 der oberen Zahl weg.

- Schritt 2a: Neben jede Ziffer 3 der unteren Zahl schreibt man die obere Zahl
  (ohne Anfangs-1) mit Pluszeichen.
  Schritt 2b: Neben jede Ziffer 1 der unteren Zahl   (außer der Anfangs-1)
  schreibt man die obere Zahl (ohne Anfangs-1) mit Minuszeichen.

- Schritt 3: Zur Vereinfachung dieser Addition(en) / Subtraktion(en) kann man
  sich gegenseitig aufhebende Ziffern oder Teilstriche streichen, wie oben im
  Abschnitt über Subtraktion erklärt.

- Schritt 4: Man führt die hingeschriebenen Addition(en) / Subtraktion(en) durch.


Damit ist die Multiplikation bereits beendet. Im Beispiel waren (außer dem trivialen Übereinanderstellen) nur 1 Addition und 1 Subtraktion nötig, die zudem durch Streichen vereinfacht wurden.       Wenn man beide Zahlen vertauscht, ist sogar nur 1 Subtraktion (jetzt einer 3-stelligen Zahl) nötig.

Bei einer n-stelligen unteren Zahl sind im ungünstigsten Fall (wenn sie keine Ziffern 2 enthält) n-1 Additionen oder Subtraktionen durchzuführen (zur Anfangs-1 wird nie addiert). Bei anderen Zahlensystemen (außer dem Zweiersystem, bei dem die Zahlen für menschlichen Gebrauch eindeutig zu lang sind), sind dagegen n Multiplikationen Zahl * Ziffer nötig sowie n-1 Additionen.



Variation 1:
Eigentlich ist es günstiger, die zu addierenden Zahlen (Schritt 2a, Plus) rechts neben die 2 übereinandergestellten Zahlen zu stellen, die zu subtrahierenden Zahlen (Schritt 2a, Minus) links neben die 2 übereinandergestellten Zahlen (auf die Seite der Einsen in dieser Zahl). Dann verwechselt man beim Zusammenrechnen nicht so leicht Plus und Minus, und die waagrechte Position der Ziffern relativ zu den übereinandergestellten 2 Zahlen ist besser erkennbar, weil der Abstand oft geringer ist. Nachteilig ist dann aber, daß man von vornherein links Platz lassen muß für die zu subtrahierenden Zahlen; der Platzbedarf kann aber durch Zählen der Einsen der unteren Zahl leicht bestimmt werden.

Variation 2:
- In obigem Beispiel erzeugt die Ziffernfolge 31 in der unteren Zahl eine Addition und eine Subtraktion der oberen Zahl. Das könnte man durch 2 Additionen der oberen Zahl (auf Höhe der 1) ersetzen, denn 3-1 = 2 (die addierte Zahl 1 Stelle höher hatte den 3fachen Zahlwert).
- Ähnlich könnte man bei einer Ziffernolge 13 in der unteren Zahl die Addition und Subtraktion durch 2 Subtraktionen (auf Höhe der 3) ersetzen.
- Endet die untere Zahl auf 1, so kann man das Überstellen der oberen Zahl und Abziehen dieser Zahl auf Höhe der 1 ersetzen durch 2 Additionen der oberen Zahl auf Höhe der 1 (denn die übergestellte Zahl hat den 3-fachen Zahlwert).


Ich frage mich, ob obiger Multiplikationsalgorithmus noch vereinfacht werden kann. Mir schwebt vor, daß man beide Zahlen übereinanderstellt (oder kammartig ineinanderschiebt) und dann nur noch in einem Zug einige Ziffern korrigiert nach irgendeiner Regel.


Es gibt leicht zu rechnende Sonderfälle, die sich direkt aus obigem Multiplikationsalgorithmus ergeben:

- Multipliziere 3-er Potenz mit Zahl:   die Zahl (ohne Anfangs-1) voranstellen (darüberstellen)
- Multipliziere 3-er Potenz mit 2:       Ziffer 1 voranstellen
- Multipliziere 3-er Potenz mit 3:       Ziffer 2 voranstellen
- Multipliziere 3-er Potenz mit 4:       Ziffer 3 voranstellen

- Multipliziere Zahl mit 3:       die Zahl (ohne Anfangs-1) der Zahl 3 voranstellen
- Multipliziere Zahl mit 4:       Zahl mit 3 multiplizieren, dazu Zahl addieren (3 +1 = 4)
- Multipliziere Zahl mit 6:       Zahl + Zahl, Ergebnis mit 3 multiplizieren (2 * 3 = 6)
- Multipliziere Zahl mit 8:       Zahl mit 9 multiplizieren, davon Zahl subtrahieren (9 - 1 = 8)
- Multipliziere Zahl mit 10:     Zahl mit 9 multiplizieren, dazu Zahl addieren (9 +1 = 10)  

Beweis des Multiplikationsverfahrens

Dieses einfache Multiplikationsverfahren ist auch einfach zu beweisen. Wir tun es für obiges Zahlenbeispiel, für alle anderen Fälle geht es ganz entsprechend.

- Beweisschritt a: Umformulierung: Wir formulieren die Zahl 33 (= 3121 im 3+1 System) um:

                       3              2 + 1
                       1              2 - 1
                       2              2
                       1   wird zu    1

Das Ganze in Strichziffern:

- Beweisschritt b: Die linke Spalte des neuen Ausdrucks, nämlich 2221, hat den Wert 27 und ist eine Potenz der Basis 3, wie alle Folgen des Typs ...221 (s.o.).   Wir multiplizieren jetzt 8 mit dieser Dreierpotenz, indem wir einfach nach der Anfangs-1 von 8 (im 3+1 System: 211) die Folge 222 einschieben (s.o. Abschnitt über Multiplikation mit 3 und Potenzen von 3).

- Beweisschritt c: Das erhaltene Ergebnis müssen wir noch korrigieren: Für jede +1 in der rechten Spalte des in Schritt a gewonnenen Ausdrucks müssen wir den Multiplikanden (hier die Zahl 8), multipliziert mit dem Stellenwert der +1, addieren.
Die Multiplikation mit dem Stellenwert geschieht einfach dadurch, daß wir die Zahl auf der Höhe der +1 beginnen lassen (Schreibrichtung der Strichziffern v.u.n.o., höherwertige Stellen stehen weiter oben!). Die beiden Einerstellen sind dabei als 1 Stelle zu betrachten (z.B. ist ...11 gleich ...2) !
Entsprechend müssen wir für jede -1 in der rechten Spalte des in Schritt a gewonnenen Ausdrucks den Multiplikanden, multipliziert mit dem Stellenwert der -1, subtrahieren.

- Beweisschritt d: Wir verschieben jede Anfangs-1 (waagrechten Strich) der in Schritt c hingeschriebenen Zahlen nach links. Das heißt wir addieren / subtrahieren sie bei der links davon stehenden Ziffer 2. Dadurch ergibt sich im unteren Teil der Gesamtzahl gerade wieder die ursprüngliche Zahl, d.h. die Umformumg aus Schritt a wird durch Schritt d wieder rückgängig gemacht.


Damit ist bewiesen, daß die in Schritt d erhaltene Formulierung, die leicht zu berechnen ist, der Multiplikation entspricht.

Zahlenumwandlung

So rechnet man eine Zahl des 3+1 Systems in eine Zehnerzahl um: Man rechnet einfach den Zahlenwert aus, d.h. man multipliziert jede Ziffer mit ihrem Stellenwert und summiert die Ergebnisse.

So rechnet man eine Zehnerzahl ins 3+1 System um:

- Man subtrahiert 1. Diese wird zur Anfangs-1
- Man führt das Divisionsverfahren durch, das bereits bei den Plus-Systemen beschrieben wurde. (wird ergänzt)

Exponentialdarstellung

Sehr große oder sehr kleine (viel kleiner als 1) Zahlen sind in jedem Zahlensystem lang. Bei runden Zahlen verwendet man dann zweckmäßigerweise die kurze, übersichtliche Exponentialdarstellung. Beispiel im Dezimalsystem:

   10 000 =  1*104    =  1e4
   0,0001 =  1*10-3   =  1e-3
   0,0022 = 22*10-4   =  22e-4

- Die kürzere Schreibweise mit mit e (für Exponent) ist in der EDV gebräuchlich
- Ein negativer Exponent, z.B. 1*10^-3 ist per Definition eine Abkürzung für 1 / (10^-3)


Diese Exponentialschreibweise hat Vorteile: Sie ist kurz. Man kann immer mit ganzen Zahlen auskommen. Man kann einfach multiplizieren: z.B. ist 2*10⁴ mal 3*10⁵ = 6*10⁹ (D.h. man multipliziert die vorderen Teile (sog. Mantisse) und addiert die Exponenten).

Auch im 3+1 System ist eine solche Exponentialdarstellung möglich und empfehlenswert. Sie ist sogar sehr kurz, wenn man die Anfangs-1 gleichzeitig als Trennzeichen verwendet.
Der Exponent steht dann unterhalb. Da es aber wünschenswert ist, daß bei unserer Strichzifferdarstellung die Einer ganz unten stehen (beim Lesen von unten, besonders beim Hören kennt man dann sofort den Stellenwert jeder Ziffer), wäre es zu überlegen, ob man die Anfangs-1 nicht ganz nach oben setzt und dann den Exponenten folgen läßt. Bei negativen Exponenten könnte man dann statt der üblichen Anfangs-1 (waagrechter Strich) einen Schrägstrich verwenden.

Nachkommastellen

Brüche kann man im 3+1 System genau wie im Dezimalsystem definieren. Auch Exponentialdarstellung ist leicht möglich, wie im vorigen Abschnitt beschrieben. Sie ist oft sinnvoller als Nachkommastellen.

Doch auch Nachkommastellen sind leicht machbar. Sie haben wie üblich die Stellenwerte b^-1, b^-2, ... (b = Basis des Zahlensystems), beim 3+1 System also die Stellenwerte 1/3, 1/9, ... Nachkommastellen lassen sich darstellen wie allgemein bei den Plus-Systemen beschrieben. Zur Abtrennung der Nachkommastellen kann statt des Kommas auch die Anfangs-1 dienen, wenn sie durch ein eigenes Zeichen dargestellt wird (wie in obigen Darstellungen durch Strichziffern), oder die Null, die sonst nicht innerhalb von Zahlen vorkommt.

Die Zahl 13 beispielsweise läßt sich nun im 3+1 System statt 331 (3*3 + 3*1 +1) auch schreiben als 3303 (3*3 +3*1 +3*1/3) oder 33023 (3*3 +3*1 +2*1/3 + 3*1/9) oder 330223 oder 3302223 oder ...
(Ähnlich wie sich im Dezimalsystem 10 auch als 10,0 oder 10,00 oder ... schreiben läßt).
Umgekehrt lassen sich gebrochene Zahlen, die auf ..3 oder ..23 oder ..223 etc. enden, immer kürzen. Der Endungtyp ..2223 repräsentiert also runde gebrochene Zahlen, so wie der Endungstyp ..2221 (entspricht wegen der 2 Einerstellen ja ..223) runde ganze Zahlen repräsentiert.

Weshalb haben wir als Trennzeichen gerade die Null gewählt? Weil man dann kein neues Zeichen benötigt, und weil die Null manchmal sowieso gehäuft am Beginn der Nachkommastellen auftritt. Beispiel:
Der Wert 1/27 lautet im 3+1 System (mit Komma als Trennzeichen) ,001 und läßt sich also nur mit mehreren Nullen darstellen. Mit Null als Trennzeichen lautet er 0001


Auch Sonderlösungen sind denkbar, z.B. die Nachkommastellen als Potenzen von 4 (nicht 3) zu definieren und an jeder Nachkommastelle die Ziffern 0 bis 3 zu erlauben. Man rechnet dann nach dem Komma im normalen Zahlensystem zur Basis 4

Vor- und Nachteile

Es gelten allgemein die Vort- und Nachteile der Plus-Systeme.   Speziell für das 3+1 System gilt:

- Jede Zahl der Form ..331 gibt exakt die Anzahl der Knoten in einem Dreierbaum (= Ternärbaum: Graph mit 1 Wurzelknoten und je 3 Nachfolgern pro Knoten) an. Die Ziffernzahl gibt die Anzahl der Ebenen des Graphen an. Beispiele:





Der Zahl 331 (dezimal 13) entspricht also ein Dreierbaum mit 3 Ebenen und 13 Knoten (3*3 + 3*1 +1). Die Anfangs-1 ist sozusagen der Wurzelknoten.
Jeder Zahl mit n Ziffern entspricht genau 1 Weg im Dreierbaum mit n Ebenen. Im Bild rechts ist 111 der Weg ganz links, 222 der mittlere (senkrechte) Weg, 333 der Weg ganz rechts. (Wenn man definiert: 1= links 2 = Mitte 3 = rechts, was sinnvoll erscheint, da bei unserer Strichzifferdarstellung der senkrechte 1-Strich ganz links im Zeichenfeld sitzt, die 2 bis zur Mitte reicht, die 3 bis an den rechten Rand).

Im Zehnersystem lassen sich Dreier-Bäume zwar genauso durchnumerieren. Doch bleiben Lücken in der Numerierung: Zahlen mit Ziffern 0 und 4-9 werden nicht verwendet.



Weitere Vor- und Nachteile des 3+1 Systems:

- Die Basis 3 ist eine Primzahl. Das hat zur Folge, daß Brüche mit einer Potenz der Basis im Nenner nie gekürzt werden müssen (außer durch 3 und Potenzen davon), und Nachkommastellen direkt als nicht kürzbarer Bruch geschrieben werden können. Dagegen muß z.B. im Dezimalsystem 2/10 auf 1/5 gekürzt werden, bis der Bruch die minimale Form hat.

- Die Basis 3 ähnelt Pi = 3,14: Rechnungen mit Pi lassen sich also leicht näherungsweise durchführen.

- Dagegen lassen sich gebrochene Zahlen nicht immer ohne Rundungsfehler ins Binärsystem und andere Zahlensysteme mit Zweierpotenz als Basis wandeln. (Diesen Nachteil hat aber auch das Dezimalsystem).

- Die kleine Basis 3 macht Rechnen einfach und schnell erlernbar, wegen des kleinen Einmaleins. Auch weil Strichziffern praktikabel sind und das rechnen anschaulich machen, z.B. auch mit Hölzchen.

- Besonders hervorzuheben ist die einfache Multiplikation, die quasi ohne Multiplizieren auskommt, nur mit Addition und Subtraktion. Insgesamt ist die einfache Erlernbarkeit und Rechenbarkeit ein sehr wichtiger Gesichtspunkt: viele Menschen in Entwicklungsländern können nicht rechnen!

- Die Zahlen sind wegen der kleinen Basis gut strukturiert. Allerdings sind sie relativ lang, was aber auch einen Vorteil hat: Man kann sie ggf. leichter an der Länge unterscheiden (Strichziffern als Blockdiagramm).

Man erkennt am 3+1 System, daß die optische Repräsentation eines Zahlensystems (Zifferngestaltung, Strichziffern) sowie die akustische Repräsentation (kurze Silben für die Ziffern, hier unbedingte Forderung) für die Anwendbarkeit eines Zahlensystems entscheidend sein können.

3+1 System und Bilderschrift

Bei einer Bilderschrift, z.B. der Lautbildschrift, wo Zahlen durch Strichziffern dargestellt werden, hat das 3+1 System folgende Eigenheit:
Die Anfangs-1 repräsentiert sozusagen ein Ding, die anderen Ziffern seine Vervielfältigung. Stellt man in der Bilderschrift eine Zahl über das Ideogramm eines Dings, so läßt man deshalb die Anfangs-1 weg. Zur Darstellung des Sachverhalts "4 Kreise" malt man also einen Kreis und drei Striche darüber.



Das hat den Vorteil, daß man tatsächlich nur 4 Elemente sieht - 1 Kreis und 3 Striche, von denen jeder 1 weiteren (quasi verkleinerten, in der Entfernung undeutlichen) Kreis repräsentiert. (Bei Verwendung eines normalen Zahlensystems würde man 4 Striche über den Kreis stellen und sähe dann fälschlicherweise insgesamt 5 Elemente).
Der Multiplikationsalgorithmus wird dann noch einfacher: Das Abstreifen der Anfangs-1 entfällt, man stellt einfach beide Zahlen hintereinander über das Ideogramm und führt noch die nötigen Additionen / Subtraktionen durch. Der Additionsalgoritmus wird aber komplizierter, da man auch die 2 dargestellten Dinge berücksichtigen muß (wie vorher die Anfangs-1).



Anhang: Andere +1 Zahlensysteme

Die Benutzung der hier beschriebenen Techniken ist frei                 Stand: 22.2.06

Autor und Erfinder: Leonhard Heinzmann                                            Homepage