Das Teilermosaik
Kurzübersicht
Das Teilermosaik ist ein Diagramm des Figuren-Rechnens (Figurale Arithmetik),
an dem die Teiler einer Zahl ablesbar sind. Es war schon Platon bekannt (s.u.)
Aufbau
Das Teilermosaik ist so aufgebaut:

- Zeile 1 ist eine Reihe von Punkten. Ihnen entsprechen die Zahlen 1, 2, 3, 4 ...
- Zeile 2 beginnt mit einem Punkt über der 2, die Punkte folgen im Abstand 2 aufeinander
- Zeile 3 beginnt mit einem Punkt über der 3, die Punkte folgen im Abstand 3 aufeinander
Zeile 1 symbolisiert also alle durch 1 teilbaren Zahlen, Zeile 2 alle durch 2 teilbaren Zahlen,
Zeile 3 alle durch 3 teilbaren Zahlen.
Man kann das Mosaik weiter aufbauen, es ist prinzipiell nach rechts und oben unbegrenzt.
Das folgende Mosaik ist rechts nach der Zahl 60, oben nach Reihe 20 abgeschnitten:
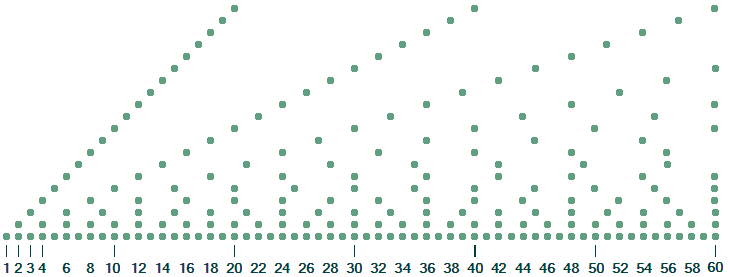
Erkennen von Teilern einer Zahl
Es ist leicht, an diesem Diagramm die Teiler einer Zahl zu erkennen:
- Man sucht die Zahl auf der 1-er Linie und geht senkrecht nach oben (rote Linie).
Alle Punkte auf der senkrechten Linie repräsentieren einen Teiler.
Man sieht, daß z.B. die Zahl 8 die Teiler 1, 2, 4, 8 hat.
12 hat die Teiler 1, 2, 3, 4, 6, 12 - man erkennt gleich an den vielen
Punkten, daß es eine hoch zusammengesetzte Zahl ist. Genauso erkennt man leicht,
daß 17 eine Primzahl ist - auf ihrer senkrechten Linie sind keine Zwischenpunkte <17
Der unterste und der oberste Punkt der senkrechten Linie symbolisieren
immer die beiden unechten Teiler einer Zahl, nämlich 1 und die Zahl selbst.
Genauso symbolisieren der n-te Punkt von unten und der n-te Punkt von oben
immer 2 komplementäre Teiler der Zahl (ihr Produkt ist die Zahl).
- Zur besseren Identifizierung eines Punkts auf einer senkrechten Linie (welche Zahl repräsentiert er?)
geht man waagrecht nach links (waagrechte blaue Linie im Bild unten) bis zur linkesten Schräglinie.
Dann zählt man vom Diagrammursprung (die 1 links unten) aus die Punkte auf der Schräglinie bis zur waagrechten Linie,
oder man geht senkrecht nach unten (senkrechte blaue Linie) und zählt von links her die Punkte auf der untersten waagrechten Linie.
Letzteres Verfahren hat den Vorteil, daß man gleich die Teiler des identifizierten Punkts erkennt,
sie liegen alle auf der senkrechten blauen Linie.

Primzahlen und Quadratzahlen
Man könnte Primzahlen anders einfärben (hier dunkelblau),
um das Mosaik aussagekräftiger zu machen.
Auch Quadratzahlen könnte man entsprechend kennzeichnen (hier als Kringel),
evtl. auch höhere Potenzen oder alle Zweierpotenzen.

Bild oben: Markiert wurden Primzahlen und Quadratzahlen auf der Grundlinie und der Schräglinie ganz links.
Auf letzterer sind Seitenabstand vom Nullpunkt aus und Höhenabstand von der Grundlinie aus gleich.
Man könnte diese Zahlen auch auch auf den senkrechten Linien markieren,
z.B. die 4 in Spalte 16

Im Bild oben haben wir die Primzahlen überall markiert (z.B. die 3 in Spalte 9)
und einige Spalten durch senkrechte farbige Linien verdeutlicht, entsprechend ihrer Zahl ganz unten
(rot: Quadratzahlen, blau: Vielfache von 10). Nun kann man leicht folgende Sätze erkennen:
- Hat eine Zahl mehr als 2 (echte) Teiler, so sind nicht alle prim
- Bereits bei 3 Teilern ist mindestens die Hälfte nicht prim
Die Anzahl der nichtprimen Teiler berechnet man nach den Regeln der Kombinatorik,
wobei zu berücksichtigen ist, daß Teiler auch in höherer Potenz vorkommen können
- Eine Zahl ist genau dann eine Quadratzahl, wenn sie eine ungerade Zahl von Teilern hat
- Der mittigste Teiler ist die Wurzel der Zahl.
Addition und Subtraktion
Wie bereits im Artikel Figuren-Rechnen gezeigt,
lassen sich Addition und Subtraktion sehr einfach darstellen und durchführen.
Bei der Addition von 2 Zahlen werden einfach 2 "Perlenketten" aneinandergereiht.
Im Teilermosaik geht man hierzu auf der Grundlinie, der 1-er Linie, zur 1. Zahl
und geht um die der 2. Zahl entsprechende Anzahl Punkte nach rechts.
Bei der Subtraktion geht man von der ersten Zahl aus um die entsprechende Anzahl Punkte nach links.
Ist der Subtrahend größer als der Minuend, so vertauscht man zunächst beide
und stellt vor das Ergebnis ein Minuszeichen.
Multiplikation und Division
Auch Multiplikation von 2 Zahlen läßt sich am Teilerdiagramm einfach darstellen
und durchführen, allerdings etwas anders als beim üblichen Figuren-Rechnen.
Beispiel 3*5: Man geht auf der Grundlinie zum ersten Faktor, hier 3, geht hoch bis zur 3-er-Linie,
geht auf dieser um 5 Punkte (einschl. Startpunkt) nach rechts, und zum Schluß wieder nach unten zur Grundlinie
(rote Linie). Der gefundene Punkt 15 ist das Ergebnis der Multiplikation.

Bei der Division macht man es umgekehrt. Beispiel 15/5 : Man geht von der 15 hoch zur 5-er-Linie,
geht von dort zur linkesten Schräglinie und zählt die Punkte auf diesem waagrechten Weg, ihre Anzahl ist das Ergebnis, hier 3
Wiederholung von Mustern
- Innerhalb jeder Zeile wiederholt sich ein Muster.
Z.B. wiederholt sich in Zeile 3 das Muster "leer - leer - Punkt".
Man könnte es auch als mittelsymmetrisches Muster "leer- Punkt - leer" auffassen,
dann beginnt es aber nicht ganz links.
- Auch zeilenüberlappend wiederholen sich Muster. Sie sind kgV Punkte breit
(kleinstes gemeinsames Vielfache der Zeilen-Nummern).
Z.B. wiederholt sich in den Zeilen 1, 2, 3 zusammen immer nach 6 Punkten dasselbe Muster.
Wir haben in der folgenden Abbildung das erste Muster rot, das zweite orange gefärbt
(zur besseren Erkennbarkeit des Einzelmusters).
Nimmt man zum zweiten Muster noch die letzte Spalte des ersten dazu, dann hat man wieder
ein mittelsymmetrisches Muster (blau, links), in das man die Zeilen 1 bis 3 unterteilen könnte.
Das Muster ist 7 Punkte breit und überlappt sich mit dem folgenden gleichen Muster um jeweils 1 Spalte.
Man kann ein zweites mittelsymmetrisches Muster erkennen (blau, rechts).
Das eine symmetrische Muster wird zum anderen, indem man es an der Mittelsenkrechten auftrennt
und die beiden Hälften seitlich umgeklappt zusammensetzt.
Beide symmetrische Muster überlagern sich um die Hälfte ihrer Breite
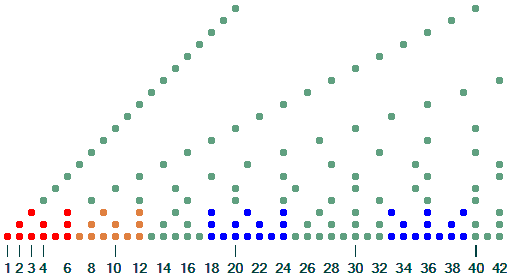
Muster müssen nicht unten in Zeile 1 beginnen. Das folgende Muster (rot) liegt in den
Zeilen 3 und 4 und ist deshalb 3*4 = 12 Punkte breit. Auch hier kann man wieder
mittelsymmetrische Muster erkennen (blau, nur 1 Version markiert)

Ab der Zahl 12 wiederholt sich auf den untersten 4 Linien (welche die Zahlen 1 bis 4 repräsentieren)
ein Muster der Breite 12 (= kgV von 1, 2, 3, 4), hier nicht markiert.
Sein rechter und linker Rand sind je 4 Punkte übereinander in den Zeilen 1 bis 4
Ebenso würde sich ab der Zahl 60 auf den untersten 5 Linien ein Muster der Breite 60
(= kgV von 1, 2, 3, 4, 5) wiederholen, usw.
Sein rechter und linker Rand sind je 5 Punkte übereinander in den Zeilen 1 bis 5
Prinzipiell lassen sich Muster und ihre Wiederholungen auf der folgenden verdoppelten und gedrehten Abbildung
leichter erkennen.
Verdoppeln und Drehen
Man kann das Teilermosaik nach unten spiegelnd verdoppeln.
Es repräsentiert dann auch die negativen ganzen Zahlen und ihre Teiler.
Um 90 Grad nach rechts gedreht sieht das verdoppelte Teilermosaik so aus:

Es ist eine durchaus künstlerisch wirkende Grafik, trotz ihres mathematisch-systematischen
Aufbaus: Man weiß, daß Mathematik und Kunst nicht unbedingt ein Widerspruch sind,
z.B. auch bei der Tonleiter.
Prinzipiell ist das Mosaik seitlich und nach unten unbegrenzt. Die seitlichen Schräglinien
müssten alle bis zum "Boden" reichen, sind aber aus Platzgründen gekürzt.
Man kann das verdoppelte Teilermosaik auch so drehen, daß die Spitze nach unten zeigt.
Dann ist eher vorstellbar, daß die Fächerstrahlen nach oben unbegrenzt sind.
Das Mosaik erinnert dann eher an die aufgehende Sonne als an einen Nadelbaum.
Historisches
Figuren-Rechnen war schon den antiken Griechen bekannt, ist aber vermutlich älter.
Daß Platon wohl auch das Teilermosaik gekannt hat, zeigt das am Anfang seines Buches
"Kratylos" eincodierte Gesicht (links):

Es erinnert an die vielen ähnlichen Gesichter (einige rot und orange hervorgehoben),
die man bei näherem Betrachten im Teilermosaik erkennen kann.
Es sieht zwar nach Jux aus, enthält aber viele signifikante Informationen,
wie im Artikel
Eincodierte Punktebilder bei Platon erklärt wird.
Bewertung
Das Teilermosaik ist, wie Figuren-Rechnen allgemein,
eine didaktisch-spielerische Angelegenheit, die aber durchaus tiefe Erkenntnisse
verdeutlichen kann. Als Rechenhilfe ist es zu aufwendig und eher unbedeutend,
könnte aber in einfachen Kulturen dafür benutzt worden sein.
Aber die Mustererkennung und -Wiederholung könnten Hinweise zur Faktorisierung von Zahlen
über die dargestellte Zahlenmenge hinaus liefern.
Die Benutzung der hier beschriebenen Techniken ist frei Stand: 16. 1. 2017 Homepage









