Tonleiter

Tonleiter

Dieser Artikel erklärt kurz und klar:

- Was ist ein Ton
- Was ist eine Tonleiter
- Warum benutzt man eine Tonleiter
- Was ist eine gute Tonleiter
- Wie konstruiert man eine gute Tonleiter

- Was sind harmonische Tonpaare

Was ist ein Ton

Ein Ton ist ein Geräusch mit einer bestimmten konstanten Frequenz (z.B. 120 Hz)

Was ist eine Tonleiter

Eine Tonleiter ist eine Auswahl von wenigen Tönen (Frequenzen) aus dem vom Menschen hörbaren Frequenzbereich, die nach Tonhöhe (Frequenz) geordnet sind. Mit diesen ausgewählten Tönen werden Melodien gebildet

Warum benutzt man eine Tonleiter

und benutzt beim Komponieren und Spielen nicht beliebige Töne? Weil es nötig ist, sich auf wenige Töne zu beschränken. Denn wenn jeder x-beliebige Ton (Frequenz) in einer Melodie vorkommen dürfte, hätte man folgende Probleme:

1) Die wenigsten Musikinstrumente können alle Töne (in einem bestimmten Frequenzbereich) hervorbringen. Im westlichen Kulturkreis sind dies nur Posaune und Geige (und der Computer) - und gerade diese sind schwer erlernbar und spielbar. Denn es ist z.B. schwierig, die genaue Auszuglänge einer Posaune für einen bestimmten Ton zu finden.
Aber andere Instrumente können eine Melodie mit beliebigen Frequenzen nicht spielen !

2) Auch gedanklich ist eine Melodie aus beliebigen Frequenzen schwer zu beherrschen: Beim Komponieren, Niederschreiben, Erlernen, Erinnern und beim Spielen tut man sich mit einer Auswahl aus nur wenigen Tönen viel leichter. Z.B. wären für beliebige Frequenzen Notenlinien unpraktikabel, man müßte mit langen Zahlen arbeiten

Was ist eine gute Tonleiter

Wie konstruiert man eine gute Tonleiter

. . Frequenzbereich

Ein Mensch kann Töne von etwa 16 - 16000 (- 20000) Hz wahrnehmen, im Alter sinkt die obere Hörschwelle meist deutlich. Die Musikwahrnehmbarkeit reicht von etwa 50 - 9000 Hz, die Sprachwahrnehmbarkeit von etwa 80 - 12000 Hz (wichtig 1900 - 4900 Hz).
Innerhalb dieser Grenzen sollte also die Musiktöne liegen. Erfahrungsgemäß reicht ein viel kleinerer Bereich: Volkslieder umfassen oft nur 1 Frequenzverdopplung, z.B. 260 - 520 Hz

Eine Tonleiter ist eigentlich frequenzunabhängig, genauso wie die Proportion zweier Töne. Das Charakteristische sind die Proportionen der leitereigenen Töne zueinander. So wie eine Melodie prinzipell dieselbe ist, egal ob sie von einer dunklen Männerstimme oder einer von einer hellen Frauenstimme gesungen wird

. . Anzahl Töne

Die Erfahrung zeigt, dass bei Volksliedern oft 8 Töne für eine sehr schöne Melodie ausreichen.
Für kompliziertere Werke braucht man mehr.

Die Anzahl der möglichen Tonpaare wächst stark mit der Anzahl der Töne ( 1 * 2 * 3 * 4 * 5 ... ).
Damit wächst auch die Zahl der möglichen harmonischen Tonpaare, aber nicht genau proportional, sie hängt auch ab von:

- der genauen Anzahl der Töne (Teilbarkeit dieser Zahl durch 2, 3, 4, 5)
- vom Typ der Unterteilung (konstanter oder zunehmender Frequenzabstand)

. . Grundton und verdoppelter Ton

Wir gehen aus vom gewünschten tiefsten Ton, dem Grundton mit Frequenz F. Nimmt man den Ton mit Frequenz 2F hinzu, dann kann man die Tonfolge oder den Akkord mit der harmonischsten Proportion bilden:

       1F : 2F  =  1:2

Fazit: Eine Tonleiter mit Grundton F sollte auf jeden Fall den Ton mit Frequenz 2F enthalten

Wir beschränken die weiteren Überlegungen zunächst auf die Unterteilung dieses Frequenzbereichs. Wenn nötig, kann man an die so gewonnene Tonleiter noch eine weitere (oder einen Teilabschnitt) anhängen, indem man den Frequenzbereich 2F - 4F genauso unterteilt.

. . Halbierung

Nimmt man außer den Tönen F und 2F noch deren Mittelton 1.5 F dazu, dann kann man Tonfolgen / Akkorde mit folgenden Frequenzverhältnissen bilden:

       1F : 1.5F  =  2:3        1.5F : 2F  =  3:4

Das sind die zweit- und dritt-harmonischste Proportion.
Fazit: eine Tonleiter sollte unbedingt den Mittelton enthalten

. . Viertelung

Nimmt man noch die Töne 5/4 F und 7/4 F dazu, dann hat man den Frequenzbereich in 4 gleiche Abschnitte unterteilt. Jetzt kann man auch Tonfolgen / Akkorde mit folgenden Frequenzverhältnissen bilden:

      1F : 1.25F  =  4:5        1.25F : 1.5F  = 5:6         1.75F : 2F = 7:8
      1F : 1.75F  =  4:7        1.25F : 1.75F = 5:7
                                1.25F : 2F    = 5:8

Das sind harmonische Tonproportionen, nur 7:8 gilt bereits als disharmonisch, kann aber trotzdem in Melodien als Spannungsgeber nützlich sein
Fazit: eine Tonleiter sollte unbedingt diese Vierteilung enthalten

. . Drittelung

Unterteilt man den Frequenzbereich F - 2F in 3 gleiche Teile, nimmt also zu den Tönen F und 2F noch die Töne 4/3 F und 5/3 F hinzu, dann kann man (auch ohne Halbierung und Viertelung) Tonfolgen / Akkorde mit folgenden Frequenzverhältnissen bilden:

      1F : 1.33F  =  3:4        1.33F : 1.66F  = 4:5           1.66F : 2F = 5:6
      1F : 1.66F  =  3:5        1.33F : 2F     = 4:6 = 2:3

Man gewinnt also 2 weitere Tonkombinationen mit den sehr harmonischen Proportionen 2:3 und 3:4 (andere als bei Halbierung) und 2 weitere Tonkombinationen mit den harmonischen Proportionen 4:5 und 5:6 (andere als bei Viertelung). Außerdem die harmonische Kombination 3:5, die innerhalb einer Frequenzverdopplung nur mit Drittelung zu erreichen ist
Zusammen mit den Tönen der Viertelung erhält man weitere meist harmonische Tonkombinationen.
Fazit: eine Tonleiter sollte unbedingt diese Dreiteilung enthalten

. . Siebenteilung (ungleich)

Eine Tonleiter sollte also die Töne der Viertelung und Drittelung enthalten. Man hat dann eine Tonleiter mit 7 Tönen und mit 6 zum Teil ungleichen Abschnitten. Damit läßt sich schon gute Musik machen, denn es lassen sich alle oben erwähnten harmonischen Tonpaare bilden, sowie weitere, z.B.:

       1.25F : 1.66F  =  3:4

Fazit: eine Tonleiter sollte unbedingt diese Siebenteilung enthalten

. . Zwölfteilung

Trotzdem liegt es nahe, die Viertelung und Drittelung zu systematisieren und den Frequenzbereich in 12 gleiche Abschnitte zu unterteilen, denn 12 ist die kleinste Zahl, die durch 3 und 4 teilbar ist
Mit F und 12 weiteren Tönen im Abstand von je 1/12F kann man alle Töne und damit alle Tonkombinationen der halbierten, geviertelten und gedrittelten Tonleiter bilden, z.B.:

      1F : 18/12F  =  12:18  =  2 : 3
      1F : 20/12F  =  12:20  =  3 : 5

Viele weitere brauchbare Tonkombinationen sind möglich, z.B.:

      1F : 15/12F  =  12:15  =  4 : 5
      1F : 14/12F  =  12:14  =  6 : 7

Fazit: die Zwölfteilung ist für eine Tonleiter nützlich, aber nicht unbedingt nötig

. . Unterteilung in Zahl mit vielen Teilern

Prinzipiell sollte der Bereich der Frequenzverdopplung F - 2F nicht in eine Primzahl unterteilt werden, sondern in eine Zahl mit möglichst vielen Teilern (hoch zusammengesetzte Zahl)
Denn dann ergeben sich, vom Grundton F ausgehend, viele harmonische Tonkombinationen (also solche mit niedrigen Brüchen als Frequenzverhältnis), weil sich viele Frequenzpaare kürzen lassen

Beispiel: Unterteilt man die Frequenzverdopplung F - 2F in 12 gleiche Abschnitte, dann ergibt (wie bereits oben gezeigt) das Tonpaar "F : (F + 6/12 F)" das harmonische Frequenzverhältnis 12:18 = 2:3 . Ja, alle Frequenzpaare F : (F + X/12 F) sind kürzbar außer bei X = 1, 5, 7, 11

Aber wenn man die Frequenzverdopplung F - 2F in 11 (Primzahl) gleiche Abschnitte unterteilt, dann ergibt kein Tonpaar "Grundton - höherer Ton" ein kürzbares Frequenzverhältnis. Alle diese Tonpaare sind deshalb disharmonisch, z.B. 11:12, 11:13, ... außer F:2F = 1:2

Allerdings lassen sich auch bei Unterteilung der Frequenzverdopplung in 11 gleiche Abschnitte harmonische Tonpaare bilden, aber nicht vom Grundton aus. Z.B. läßt sich das Frequenzverhältnis 2:3 erzeugen durch das Tonpaar (F + 1/11) : (F + 7/11) = (12/11):(18/11) = 12:18 = 2:3

Die folgende Tabelle zeigt die Leistungsfähigkeit von Tonleitern mit Unterteilung des Tonbereichs "Grundfrequenz - doppelte Frequenz" in 4 bis 12 gleiche Abschnitte. Jede Zeile repräsentiert 1 harmonisches Frequenzverhältnis, jede Spalte repräsentiert 1 Tonleiter (die rechteste, gelbe Spalte die Tonleiter mit 12 Abschnitten). Jedes Kästchen im Kreuzungspunkt einer Spalte und Zeile zeigt die Tonkombinationen, mit denen man dieses Frequenzverhältnis in dieser Tonleiter erzeugen kann
[Zur Tonbenennung: in der Tonleiter mit 4 Abschnitten bezeichnet 4 den Grundton, 5, 6, 7, 8 die nächsten Töne - 8 ist der doppelte Grundton. So kann man leicht erkennen, welche Tonpaare sich kürzen lassen.
Entsprechend bei den anderen Tonleitern]

Frequenz-
Verhältnis Unterteilung des Tonbereichs "Grundfrequenz bis doppelte Frequenz"
in wieviel gleiche Abschnitte
4 5 6 7 8 9 10 11 12

1 : 2 4:8 5 : 10 6 : 12 7 : 14 8 : 16 9 : 18 10 : 20 11 : 22 12 : 24
2 : 3 4:6 6 : 9 6 : 9
8 : 12
8 : 12
8 : 12
10 : 15

10 : 15
12 : 18

10 : 15
12 : 18

12 : 18
14 : 21

12 : 18
14 : 21
16 : 24
3 : 4 6:8 6 : 8 6 : 8
9 : 12
9 : 12
9 : 12
12 : 16
9 : 12
12 : 16

12 : 16
15 : 20

12 : 16
15 : 20

12 : 16
15 : 20
18 : 24
3 : 5 6 : 10 6 : 10
9 : 15
9 : 15

12 : 20

12 : 20

12 : 20
4 : 5 4:5 8 : 10 8 : 10 8 : 10 8 : 10
12 : 15
12 : 15
12 : 15
16 : 20
12 : 15
16 : 20
12 : 15
16 : 20
5 : 6 5:6 5 : 6
10 : 12
10 : 12
10 : 12
10 : 12
15 : 18
10 : 12
15 : 18

15 : 18

15 : 18
20 : 24
5 : 8 5:8 5 : 8
10 : 16
10 : 16
10 : 16

15 : 24

Fazit:
Man sieht, daß die Tonleitern mit Anzahl Abschnitte = Primzahl > 5 (also 7, 11) nicht mehr harmonische Frequenzverhältnisse ermöglichen als die mit einem Ton weniger (also mit 6 oder 10 Abschnitten), sondern sogar weniger
Auch eine Tonleiter mit 8 gleichen Abschnitten ist insgesamt etwas harmonischer als eine mit 9. Grund: Die Zahl 8 hat 2 Teiler (2,4), die Zahl 9 nur einen, nämlich 3 . Bei 9 Abschnitten können also weniger Tonpaare auf ein ein einfaches harmonisches Frequenzverhältnis gekürzt werden

Folgen von harmonischen Tonpaaren:
Ein weiteres Bewertungskriterium von Tonleitern ist, wie viele und wie lange Folgen von Tönen sich bilden lassen, bei denen jeder Ton mit dem nächsten in einem harmonischen Frequenzverhältnis ist. Das hängt natürlich von der Anzahl möglicher harmonischer Tonpaare ab, aber auch davon. wie gut diese zusammenpassen

Beispiel: bei einer Tonleiter mit 12 gleichen Abschnitten haben die Töne 12, 18, 24 zueinander das Verhältnis 2:3 und 3:4, die Töne 12, 16, 20, 24 haben die Verhältnisse 3:4, 4:5, 5:6, die Töne 12, 18, 21 haben die Verhältnisse 2:3, 5:7

Bei Tonleitern mit Abschnittsanzahl = Primzahl gibt es weniger Möglichkeiten zur Bildung von solchen harmonischen Tonfolgen, weil vom Grundton aus keine harmonische Proportion möglich ist (außer 5:6 bei einer Tonleiter mit nur 5 Abschnitten, und 6:7 bei einer Tonleiter mit 6 Abschnitten)

Wir haben im obigen Beispiel nur die steigenden harmonischen Tonfolgen aufgezählt, da ist die Länge sehr begrenzt. Aber es gibt auch harmonische Tonfolgen mit abwechselnd steigenden und fallenden Abschnitten. Doch sind ganze Melodien mit ausschließlich harmonischen Tonpaaren fast unmöglich - die disharmonischen Tonpaare wirken auch als Spannungsgeber

Bisher haben wir die Frequenzverdopplung F - 2F in gleiche Abschnitte unterteilt (außer bei der Siebenteilung). Doch es gibt auch andere Möglichkeiten. Hier allgemein die Prinzipien:

. . 2 Prinzipien der Unterteilung

Man will die Töne einer Leiter so festlegen, daß möglichst viele harmonische Tonpaare möglich sind (siehe oben). Zu diesem Zweck haben sich 2 Prinzipien als nützlich herausgestellt:

- gleiche Frequenzabstände (Differenz konstant)
- gleichmäßig zunehmende Frequenzabstände (Quotient konstant)

- speziell ausgetüftelte Frequenzabstände

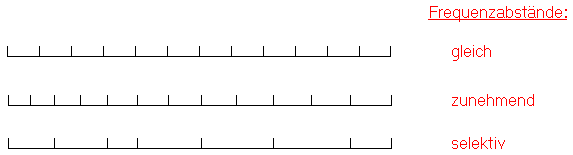
Bei gleichen Abständen hat jeder Ton zum folgenden denselben Frequenzabstand (additive Tonleiter)
Bei gleichmäßig zunehmenden Frequenzabständen hat jeder Ton zum folgenden dasselbe Frequenzverhältnis (multiplikative oder proportionale Tonleiter), also Ton1:Ton2 = Ton2:Ton3 = Ton3:Ton4 ...

Gleiche oder gleichmäßig zunehmende Frequenzabstände sind die eigentlichen 2 Grundprinzipien für eine Tonleiter
Bei anderen Tonleitern handelt es sich praktisch immer um eine Tonleiter dieser 2 Typen, bei der einige weniger nützliche Töne weggelassen wurden. So sind die bekannten europäischen Tonleitern mit 8 Tönen eigentlich Tonleitern des 2. Typs mit 12 Tönen (plus Grundton), bei denen je nach Tonart (Dur, Moll, etc.) einige weniger brauchbare Töne weggelassen sind, aber gelegentlich doch als "Halbtöne" eingeflickt werden. Das Beispiel "selektiv" im obigen Bild ist gerade die Dur-Tonleiter, die durch Auswahl der Töne 0 (Grundton), 2, 4, 5, 7, 9, 11, 12 aus der dargestellten zunehmenden Tonleiter entsteht. Und die weiter oben beschriebene Tonleiter mit Siebenteilung (ungleich) entsteht aus der Tonleiter mit 12 gleichen Abständen durch Auswahl der Töne 0 (Grundton), 3, 4, 6, 8, 9, 12
(Dabei ermöglichen die Töne 0, 3, 6, 9, 12 die Viertelung, die Töne 0, 4, 8, 12 die Drittelung, s.o.)

Ein konkretes Beispiel: Man will in dem Frequenzbereich von 240 bis 480 Hertz 12 Töne haben, um Melodien zu komponieren. (Für Volkslieder reichen dieser Bereich und diese Tonzahl aus).

Man kann sich nun eine Tonleiter mit gleichen Frequenzabständen (jeweils 20 Hz) schaffen und hat dann die Töne 240, 260, 280, . . . 440, 460, 480 Hz.

Man kann sich aber auch eine Tonleiter mit gleichmäßig zunehmenden Frequenzabständen schaffen. Dafür braucht man einen Faktor X, für den gilt:

Ton 1 = Ton 0 * X (also Grundfrequenz * X)
Ton 2 = Ton 1 * X (also Grundfrequenz * X * X, in math. Schreibweise: Grundfrequenz * X²)
Ton 3 = Ton 2 * X (also Grundfrequenz * X * X * X in math. Schreibweise: Grundfrequenz * X³)
. . .
Ton 12 = Ton 11 * X (also Grundfrequenz * X¹²)

Weil Ton 12 die 2-fache Frequenz wie Ton 0 haben soll (480 / 240 Hz), ist der gesuchte Faktor X die 12te Wurzel aus 2, also etwa 1,06

. . Vergleich der 2 Prinzipien

Welches der beiden Prinzipien zur Unterteilung einer Tonleiter ist leistungsfähiger?
Also bei welchem Prinzip lassen sich mehr harmonische Tonpaare bilden?
Gibt es noch weitere Gesichtspunkte?

Wir untersuchen zunächst die Tonleiter mit gleichen Abständen. Hier sind bei 12 Abschnitten
die harmonischen Tonpaare möglich, die schon in der vorigen Tabelle aufgelistet sind (rechte Spalte)

Wir untersuchen jetzt die proportionale Tonleiter mit 12 Abschnitten. Zunächst listen wir deren Töne 1 bis 12 auf mit ihrer (gerundeten) Proportion zum Anfangston 0 ( = Grundfrequenz) und deren angenäherter Darstellung als Bruch:

Ton:      1     2     3     4     5     6     7     8     9     10    11    12
Prop:     1,06  1,12  1.19  1.26  1,33  1,41  1,50  1,59  1,68  1,78  1,89  2
Prop~:    16:15 9:8   6:5   5:4   4:3   7:5   3:2   8:5   5:3   9:5   19:10 2:1
                                                                4:7

Man erkennt bei der proportionalen Tonleiter:

- Keine harmonische Proportion außer 2:1 ist exakt realisierbar

- Die weiteren harmonischen Proportionen sind annähernd realisierbar

Auch bei der proportionalen Tonleiter sind 12 Abschnitte optimal (wie auch bei der mit gleichen Abschnitten, s.o.). Denn hier lassen sich die wichtigsten harmonischen Proportionen am exaktesten realisieren. Bei allen anderen proportionalen Tonleitern mit 4 bis 18 Abschnitten sind die Werte weniger exakt, bei 24 Abschnitten gleich. Weiter gilt für proportionale Tonleitern:

Jede Proportion Ton x : Ton y (x ≤ y) ist kürzbar zur Proportion Ton 0 : Ton y-x
Denn es gilt ja: Ton i = (Ton 0) * Xⁱ, mit X = 12te Wurzel von 2 (s.o.) Die Proportion bleibt also erhalten, wenn jeder der 2 Töne um denselben Faktor xⁿ vergrößert oder verkleinert wird.
Aus der Kürzbarkeit folgen mehrere Dinge:

- Jede überhaupt darstellbare Proportion ist auch von Ton 0 aus realisierbar (Ton 0 : Ton i)

- Nur die oben erwähnten Proportionen sind darstellbar!

- Jede Proportion ist beliebig verschiebbar, bis einer der 2 Töne die Tonleiter verlässt
   Z.B. gilt Ton 0 : Ton 1 = Ton 1 : Ton 2 = Ton 2 : Ton 3, .. , Ton 11 : Ton 12
   und Ton 0 : Ton 2 = Ton 1 : Ton 3 = Ton 2 : Ton 4, , .. , Ton 10 : Ton 12, etc.

- Die meisten Proportionen sind vielfach realisierbar. Beispiel:
   Die Proportion 5:6 ist 10 mal realisierbar als Ton 0 : Ton 3, Ton 1 : Ton 4, ... , Ton 9 : Ton 12
   nach der Formel: "Anzahl Möglichkeiten für die Proportion Ton 0 : Ton i" = 13 - i

Wenn an die Tonleiter F-2F eine weitere Tonleiter 2F-4F mit 12 Abschnitten und demselben Faktor x angehängt wird, ändert sich an der Verschiebbarkeit nichts: Proportionen können nun auch Leiter-überlappend realisiert werden, z.B. Ton 0 : Ton 4 = Ton 10 : Ton 14
Und die Anzahl der Realisierungsmöglichkeiten einer Proportion steigt um 12. Z.B. kann die Proportion 1:2 jetzt 13 mal dargestellt werden als Ton 0 : Ton 12, Ton 1 : Ton 13, ... , Ton 13 : Ton 24
Es sind dann auch 12 weitere Proportionen darstellbar, die alle mehr als eine Frequenzverdopplung umfasssen, nämlich Ton 0 = : Ton 13, Ton 0 : Ton 14, ... , Ton 0 : Ton 24

Bewertung:

Wir zeigen zunächst in einer Tabelle, welche harmonischen Proportionen sich wie oft bei einer Tonleiter mit 12 gleichen bzw. 12 zunehmenden Abschnitten darstellen lassen. Die Werte bei gleichen Abschnitten ergeben sich aus der Tabelle weiter oben (rechte Spalte), die Werte bei ungleichen Abschnitten aus der im vorletzten Abschnitt erwähnten Formel:

Proportion mögliche Anzahl bei
12 gleichen Abschnitten mögliche Anzahl bei
12 proportionalen Abschnitten
1 : 2 1 1
2 : 3 3 6
3 : 4 3 8
3 : 5 1 4
4 : 5 2 9
5 : 6 2 10
5 : 8 1 5

Die proportionale Tonleiter bietet also viel mehr Realisierungen der harmonischen Tonkombinationen (außer von 2:1), was sich bei Anhängen einer weiteren Tonleiter (Freqenzverdopplung) noch verstärkt.
Allerdings sind ihre Tonkombinationen (außer 2:1) nicht exakt harmonisch (rein) - was bei der Tonleiter mit gleichen Abschnitten zutrifft, die deshalb einen etwas harmonischeren Klang ermöglicht

Ein weiterer Vorteil der proportionalen Tonleiter: Melodien lassen sich problemlos verschieben,
z.B. um 1 Ton erhöhen. So lassen sich z.B. in Klavierstücken erhöhte Variationen einer Tonfolge realisieren. Bei gleichen Abschnitten ist das nicht möglich, denn es gilt z.B. bei obiger Tonleiter mit 12 gleichen Abschnitten:

Ton 0 : Ton 1 = 12*(20 HZ) : 13*(20 Hz)= 12 : 13, aber
Ton 1 : Ton 2 = 13*(20 HZ) : 14*(20 Hz)= 13 : 14

Bei Instrumenten mit "fest eingebauten Tönen", z.B. Klavier, wäre also die Verschiebung einer Melodie unmöglich

Wegen dieser vielen Vorteile sind seit über 200 Jahren die westlichen Tonleitern proportional. Es handelt sich immer um Tonleitern mit 12 völlig gleichberechtigten Tönen (plus Grundton), was aber den meisten Leuten unbekannt ist (Gründe siehe das folgende Kapitel)

Aber für einfache Musikstücke, wie z.B. Volkslieder, ist u.U. wegen des reineren Klangs eine Tonleiter mit gleichen Abschnitten vorzuziehen

Traditionelle irreführende Bezeichnungen

Wie oben erwähnt, haben die heutigen westlichen Tonleitern immer 12 völlig gleichberechtigte Töne (plus Grundton). Das ist den meisten Leuten unbekannt. Dafür gibt es viele Gründe:

- Die Anzahl Töne wird verschleiert dadurch, daß von der grundlegenden systematischen, proportionalen Tonleiter mit 12 Tönen die Dur- und die Moll-Tonleitern jeweils nur 8 (teilweise verschiedene) Töne nutzen, wobei aber die anderen Töne gelegentlich als "Halbtöne" eingeflickt werden

- Die Nomenklatur, d.h. die Benennung der Töne, "Halbtöne", Intervalle, Tonleitern etc. ist geradezu chaotisch:

- - Die Töne sind unsystematisch benannt (nicht etwa in ABC-Folge). Genauso die "Halbtöne", wobei schon diese Bezeichnung irreführend ist. Zudem gibt es für die "Halbtöne" 2 Bezeichnungen, z.B. fis = ges. Auch die Klaviertastatur mit weißen und schwarzen Tasten verfestigt die Vorstellung von Tönen und "Halbtönen"

- - Die Intervalle sind unglücklich benannt, z.B. Frequenzverdopplung = "Oktave", weil bei Tonleitern mit 8 ausgewählten Tönen der achte Ton doppelt so hoch ist wie der Grundton. Bei Tonleitern mit 5 Tönen z.B. passt dieses Wort überhaupt nicht. Man hätte besser den Begriff "doppelt" verwendet. Die anderen Intervallbezeichnungen sind noch unglücklicher: Sekunde, Terz, Quarte, Quinte sind je nach Tonleiter eine andere Proportion

- - Den Begriff "gleichstufige Tonleiter" würde ein Laie wohl als "Tonleiter mit gleichen Frequenzabständen" interpretieren, weil eine Treppe gleich hohe Stufen hat. Tatsächlich aber bedeutet er in der üblichen Musik-Terminologie "Tonleiter mit gleichmäßig zunehmenden Frequenzabständen", also eine proportionale Tonleiter

Die Gründe für diese chaotische Nomenklatur sind z.T. traditionell bedingt, z.T. ergonomisch (weniger Notenlinien für 8 Töne benötigt, notfalls ein Zusatzzeichen für einen "Halbton"), zum Teil vielleicht auch kryptografisch - viele Gelehrten-Kasten in der Geschichte versuchten sich etwas abzuschotten

Anhang: Was sind harmonische Tonpaare

Das Ziel der Musik ist meist, schöne, harmonisch klingende Melodien zu schaffen. Der Wohlklang einer Melodie besteht teilweise in der Harmonie gleichzeitiger oder direkt aufeinanderfolgender Töne.

Diese Harmonie läßt sich physikalisch beschreiben: Am harmonischsten empfindet man Tonpaare mit dem Frequenzverhältnis 1:2, dann Tonpaare mit den Frequenzverhältnissen 2:3, 3:4, 3:5, 4:5, 5:6 usw., mit jeweils abnehmender Harmonie. Der Grund dafür ist einfach: je niedriger das Frequenzverhältnis (in ganzen Zahlen ausgedrückt) von 2 Tönen ist, also je geringer das kleinste gemeinsame Vielfache kgV ist, desto früher sind beide Frequenzen wieder im Gleichtakt:

- bei 1:2 nach 1 Schwingung der niedrigeren Frequenz (nach 2 Schwingungen der höheren)
- bei 2:3 nach 2 Schwingungen der niedrigeren Frequenz (nach 3 Schwingungen der höheren)
- bei 3:4 nach 3 Schwingungen der niedrigeren Frequenz (nach 4 Schwingungen der höheren)

In folgender Tabelle ist das Frequenzverhältnis von 2 Tönen umso harmonischer, je weiter oben in der Tabelle es steht. Die Tonpaare unterhalb der Leerzeile gelten bereits als disharmonisch - werden aber trotzdem in Melodien benutzt, um Spannungen zu erzeugen

Frequenz-
verhältnis kgV oberer Ton höher
um den Bruchteil: unterer Ton niedriger
um den Bruchteil:
1 : 2 2 1/1 1/2
2 : 3 6 1/2 1/3
3 : 4 12 1/3 1/4
3 : 5 15 2/3 2/5
4 : 5 20 1/4 1/5
5 : 6 30 1/5 1/6
5 : 8 40 3/5 3/8
... ... ...
5 : 9 45 4/5 4/9
8 : 9 72 1/8 1/9
8 : 15 120 7/8 7/15

Die Frequenzverhältnisse 2:4, 3:6 u.a fehlen, weil sie kürzbar sind, sie sind also gleich 1:2, 2:3 etc. Ebenso fehlen die Frequenzverhältnisse 1:3, 2:5, 3:7, 3:8, 3:10, 3:11, 3:13, 4:9 , trotz niedrigem kgV, denn sie sind nicht innerhalb einer Frequenzverdopplung (Oktave) realisierbar - solche Tonpaare wirken meist zu schrill. Auch fehlen, trotz niedrigem kgV, die Frequenzverhältnisse 4:7 und 5:7, denn sie gelten in der Musiklehre als unharmonisch, was aber z.T. subjektiv oder kulturell bedingt sein könnte. Die Proportion 6:7, ebenfalls mit niedrigem kgV, fand ich aus unbekannten Gründen in der Musiklehre nirgends erwähnt

Man könnte auf die Idee kommen, obiges Harmoniegesetz für gleichzeitige oder benachbarte Töne auf eine ganze Melodie auszuweiten, auf zweierlei Art:

- Erweiterung Man berechnet die Harmonie-Proportion auch für nicht benachbarte Töne,
z.B. auch für "Ton - übernächster Ton" oder paarweise für alle Töne einer Melodie

- Summenbildung: Man versucht, aus den einzelnen Harmonieproportionen einer Melodie einen Gesamtwert zu bilden. Doch wie? Einfach alle kgV's zusammenzählen (Summe müßte möglichst gering sein) ergibt vermutlich kein passendes Maß. Man müßte wohl jeder Proportion einen Wohlklang-Wert zuweisen und dann diese Werte addieren. Wenn man die Harmonie nicht nur für Nachbartöne bewertet, müsste man wohl nach Entfernung gewichten (z.B. 1/Abstand oder logarithmisch, also 1/ln(Abstand) )

Eine solche Formel kann sicher nicht den ganzen Wohlklang einer Melodie erfassen. (Erstaunlich ist z.B., daß die harmonischste Proportion 1:2 in Melodien kaum vorkommt. Auch wird nicht zwischen steigenden und fallenden Tonpaaren unterschieden.)

Doch ist die Wichtigkeit der harmonischen Proportion von Tönen eine Erfahrungstatsache. Man sollte diese Erfahrung ausweiten, indem man Melodien daraufhin untersucht, ob sich die Harmonie einer Melodie genauer mit obigen Erweiterungen erkennen läßt



Autor:  Leonhard Heinzmann                            Homepage                        Stand:  16. 1. 2017

Frequenz- Verhältnis	Unterteilung des Tonbereichs "Grundfrequenz bis doppelte Frequenz" in wieviel gleiche Abschnitte
	4	5	6	7	8	9	10	11	12

1 : 2	4:8	5 : 10	6 : 12	7 : 14	8 : 16	9 : 18	10 : 20	11 : 22	12 : 24
2 : 3	4:6	6 : 9	6 : 9 8 : 12	8 : 12	8 : 12 10 : 15	10 : 15 12 : 18	10 : 15 12 : 18	12 : 18 14 : 21	12 : 18 14 : 21 16 : 24
3 : 4	6:8	6 : 8	6 : 8 9 : 12	9 : 12	9 : 12 12 : 16	9 : 12 12 : 16	12 : 16 15 : 20	12 : 16 15 : 20	12 : 16 15 : 20 18 : 24
3 : 5		6 : 10	6 : 10		9 : 15	9 : 15	12 : 20	12 : 20	12 : 20
4 : 5	4:5	8 : 10	8 : 10	8 : 10	8 : 10 12 : 15	12 : 15	12 : 15 16 : 20	12 : 15 16 : 20	12 : 15 16 : 20
5 : 6	5:6	5 : 6	10 : 12	10 : 12	10 : 12	10 : 12 15 : 18	10 : 12 15 : 18	15 : 18	15 : 18 20 : 24
5 : 8	5:8	5 : 8			10 : 16	10 : 16	10 : 16		15 : 24

Proportion	mögliche Anzahl bei 12 gleichen Abschnitten	mögliche Anzahl bei 12 proportionalen Abschnitten
1 : 2	1	1
2 : 3	3	6
3 : 4	3	8
3 : 5	1	4
4 : 5	2	9
5 : 6	2	10
5 : 8	1	5

Frequenz- verhältnis	kgV	oberer Ton höher um den Bruchteil:	unterer Ton niedriger um den Bruchteil:
1 : 2	2	1/1	1/2
2 : 3	6	1/2	1/3
3 : 4	12	1/3	1/4
3 : 5	15	2/3	2/5
4 : 5	20	1/4	1/5
5 : 6	30	1/5	1/6
5 : 8	40	3/5	3/8
...	...	...
5 : 9	45	4/5	4/9
8 : 9	72	1/8	1/9
8 : 15	120	7/8	7/15