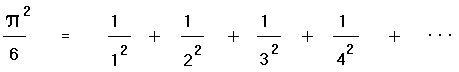
Andererseits ist der Wert der Zetafunktion für 2 gleich derselben unendlichen Reihe:
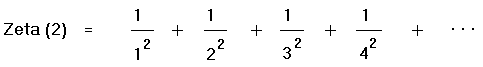
Auch bewies Euler, daß der Wert der Zetafunktion sich als unendliches Produkt ausdrücken läßt,
das für Zeta(2) folgende Form annimmt:
Dabei geht das Produkt über alle Ausdrücke der Form
in denen p eine Primzahl ist.Es gilt also:
Damit besteht also ein innerer Zusammenhang zwischen der Zahl Pi und den Primzahlen.
Der tiefere Grund dafür ist im Moment unbekannt, auch ob sich dieser Zusammenhang mathematisch-praktisch nutzen läßt, z.B. zur Faktorisierung (Zerlegung ganzer Zahlen in ihre Teiler). Kann man die Ziffern von Pi (in einem bestimmten Zahlensystem) dafür verwerten, ähnlich wie man z.B. die Ziffern von Pi im 16-er System einzeln berechnen kann (Bailey-Borwein-Plouffe Formel).
Es besteht auch ein innerer Zusammenhang zwischen den Primzahlen, der Zahl e und den trigonometrischen Funktionen. Denn die Primzahlen sind mit Pi verknüpft, Pi mit e und e mit Sinus und Cosinus nach folgenden Formeln:
