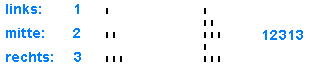Iris-Koordinaten: ein neues, einzahliges Koordinatensystem
Kurzbeschreibung
Iris-Koordinaten sind ein neuartiges radiales Koordinatensystem.
Die Positionsangabe (in der Ebene) besteht nur aus einer ganzen Zahl
(ohne Vorzeichen)! Trotzdem ist dieses System ergonomisch,
d.h. vom Menschen leicht als Position interpretierbar: Die Ziffernzahl
gibt die Entfernung eines Sektors vom Ursprung an, die Ziffernfolge
(als Verästelungen interpretiert) die Richtung.
Beispiel:
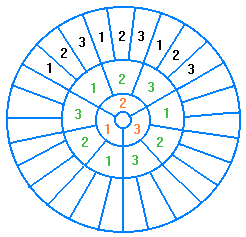
Das Bild zeigt ein Iris-Koordinatensystem mit fortwährender Dreiteilung:
Direkt um den ungeteilten Mittelkreis (er gleicht einer 0 und ist per
Definition Sektor 0) liegen 3 Sektoren mit Nummer 1,2,3.
In der nächsten Schale folgen 3 * 3 = 9 Sektoren, jeweils mit Nummern 1,2,3.
In der nächsten Schale folgen 3 * 3 * 3 = 27 Sektoren mit Nummern 1,2,3.
Es folgen beliebig viele Schalen, die jeweils die 3-fache Zahl
Sektoren wie ihre Vorgänger haben. D.h. jeder Sektor unterteilt sich
in der nächsten Schale in 3 weitere, ähnlich wie sich bei einer
Baumstruktur die Äste verzweigen.
Jeden Sektor identifiziert eindeutig eine Gesamt-Nummer, eine ganze Zahl ≥ 0.
Hat diese Zahl n Ziffern, so liegt der Sektor in Schale n (Ausnahme: Sektor 0
ist gleich Schale 0).
Die Zahl ist - von links nach rechts gelesen - eine Pfadangabe
vom Mittelkreis zu dem bestimmten Sektor:
Jede einzelne Ziffer gibt das Ziel in der nächsten Schale an.
Die Zahl 222 z.B. bedeutet:
Gehe vom Zentrum zu Sektor 2 der Schale 1. Gehe von da
(innerhalb des vorigen Öffnungswinkels bleibend) zu Sektor 2
der Schale 2. Gehe dann zu Sektor 2 der Schale 3.
Das folgende Bild zeigt Sektor 222 grün, Sektor 31 blau
und Sektor 1 gelb markiert:

Variationen: Schalenabstand
Man kann den innersten Kreis (mit Adresse 0) weglassen. Die
Positionsangabe 0 könnte man dann interpretieren als
"nirgends im Koordinatensystem".
Nach außen kann man beliebig viele Schalen um den Sektor 0 legen
und so das Koordinatensystem auf die ganze Ebene ausdehnen. Wenn
die Schalenabstände gleichgroß sind, werden aber die Sektornummern
von weit außen liegenden Punkten ziemlich lang.
Das kann man vermeiden, wenn man die Schalenradien exponentiell
vergrößert. Z.B. könnte man jeden Schalenradius dreimal so groß
machen wie den nächstinneren. Das hätte einen weiteren Effekt:
Nun ist der Außenrand aller Sektoren - gleich welcher Schale -
gleich lang. Denn nach der Formel "Kreisumfang = 2r*pi" hat sich
mit dem Radius (ab Kreismitte) auch der Umfang verdreifacht.
Weil aber jede Schale dreimal soviel Sektoren hat wie vorige,
bleibt der Außenrand jedes Sektors gleich.
(Bei fortlaufender Unterteilung in je 10 Sektoren müßte sich der Radius
jeweils verzehnfachen).
Prinzipiell entspricht ein nach außen zunehmender Schalenabstand
dem menschlichen, organischen Denken: Der Nahbereich ist meist
wichtiger als die entfernteren Bereiche, man richtet auf diese
kleine Fläche relativ mehr Aufmerksamkeit.
Variationen: Vervielfältigungsfaktor
Welcher Vervielfältigungsfaktor (Sektorenzunahme pro Schale) ist optimal?
Zehn erscheint viel zu hoch, zudem ist 10 nicht gleichmäßig unterteilbar.
Auch muß bedacht werden, daß der Vervielfältigungsfaktor ggf. den radialen
Streckungsfaktor bestimmt (s.o.).
Ein Vervielfältigungsfaktor 3 wie in obigem Beispiel hat einige Vorteile:
Man kann die Ziffern der Gesamt-Sektornummern direkt umschlüsseln
in umgangssprachliche Richtungsangaben: 1 = links, 2 = Mitte, 3 = rechts.
(Für die 3 Sektoren der Schale 1 sind diese Richtungsangaben absolut,
für die Schalen weiter außen relativ zur vorigen Richtung.)
Wenn man linksbündige Strichziffern benutzt
(im Dreiersystem praktikabel, im Zehnersystem nicht), so kann
man an ihrem rechtem Rand leicht dieses links - Mitte - rechts ablesen:
Der 1-Strich ist links im Zeichenfeld, die Zahl 2 reicht von links
bis zur Mitte (d.h. der 2. Strich ist in der Mitte des Zeichenfeldes),
3 reicht bis zum rechten Rand des Darstellungsfeldes (d.h. der 3. Strich
ist ganz rechts):
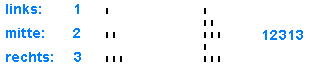
An einer Strichzahl (kleiner Stellenwert unten) kann man so leicht
den ganzen Pfadverlauf ablesen. An obiger Zahl 12313 also den Verlauf
links - Mitte - rechts - links - rechts.
Bei Vervielfältigungsfaktor 4 wird Schale 1 in 4 Teile a 90 Grad zerlegt,
was klarer und angenehmer wirkt als Dreiteilung.
Dann hat auch jeder Sektor einen genau gegenüberliegenden
(auf der anderen Seite des Kreises, um 180 Grad gedreht).
Das ist immer der Fall, wenn jede Schale eine gerade
Anzahl Sektoren hat. Und das ist bereits der Fall, wenn
nur der Vervielfältigungsfaktor n der innersten Schale
gerade ist (die äußeren Schalen haben dann die n-fache
Sektorenzahl, also auch eine gerade Zahl).
Der Vervielfältigungsfaktor verschiedener Schalen kann
nämlich auch ungleich sein. Praktikabel und sehr bemerkenswert
ist z.B. folgendes Koordinatensystem:
Innere Schale hat Faktor 4 (klare Vierteilung, jeder Sektor
hat einen gegenüberliegenden), andere Schalen haben
Faktor 3 (ergonomische Teilung in links - mitte - rechts).
(Siehe auch die Beispiele weiter hinten im
Abschnitt "Zahlenraum").
Verwendung: Koordinatensystem
Iris-Koordinaten haben folgende Eigenschaften:
1) Sie sind radial. Deshalb eignen sie sich hauptsächlich für
Positionsangaben von einem festen Zentrum aus. Wäre auf einer
Landkarte ein Iris-Koordinatensystem eingezeichnet, so wäre eine
Positionsangabe bzgl. eines anderen Mittelpunktes schwierig.
2) Die Position wird nicht punktgenau angegeben, sondern als Sektor.
Und die Positionsangabe erfolgt durch eine einzige ganze Zahl ≥ 0.
Beides zusammen macht die Positionsangabe kurz und einfach.
Geeignet wären Iris-Koordinaten z.B. zur Positionsangabe von
Objekten im Gelände, bzgl. des eigenen Standpunktes.
Auch für absolute Positionsangaben von Planeten (Sonnenabstand
und Drehwinkel, sozusagen Draufsicht auf das Planetensystem)
scheinen Iris-Koordinaten geeignet: Jeder Planet hat sozusagen
seine eigene Schale (es könnte auch leere Schalen geben), deren
Abstände regelmäßig zunehmen (nach der Titius-Bode-Regel).
3) Sektoren verschiedener Schalen haben etwas ungleiche Form.
Sie werden nach außen immer rechteckiger (nähern sich Rechteckform).
Im vorigen Beispiel werden die Sektoren nach außen auch immer länger
und schmäler - das ist abhängig von Vervielfältigungsfaktor und
Schalenabstand.
4) Eine Verfeinerung der Positionsangabe durch Nachkommastellen
macht die Sache geometrisch komplizierter: Denn um die Position
eines Punktes beliebig genau angeben zu können, genügt es ja nicht,
einen Sektor radial in immer kleinere Teilsektoren zu zerlegen:
man will auch die Entfernung beliebig genau angeben.
Bei Vervielfältigungsfaktor 4 könnte man einen Sektor kreuzförmig
in 4 Teile zerlegen, von diesen jeden wieder in 4 Teile, etc.
Bei Vervielfältigungsfaktor 3 könnte man einen Sektor mit einem
T-Schnitt in 3 Sektoren zerlegen, etc.
Man könnte auch jeden Sektor abwechselnd radial oder
tangential unterteilen (entsprechend dem Vervielfältigungsfaktor)
und entsprechend Nachkommastellen als radiale oder tangentiale
Position interpretieren.
Verwendung: Richtungsangabe
Man kann Iris-Koordinaten auch zur bloßen Richtungsangabe verwenden (ohne
Entfernungsangabe). Im Gegensatz zu einer konventionellen Winkelangabe ist dann nicht nur
die Richtung, sondern auch die Genauigkeit der Richtung bekannt: Je länger
die Zahl, desto genauer die Richtung. Z.B. bedeutet 2 ungefähr die Richtung "vorne"
(in einem 120-Grad Winkel), Richtung 22 dasselbe in einem 40-Grad Winkel,
Richtung 222 bedeutet schon ziemlich genau "geradeaus" (13-Grad Winkel).
Verwendung: Zahlenraum
Sortieren wir die in obigem Beispiel vorkommenden Sektornummern nach
ihrem Zahlenwert, so ergibt sich die Folge:
0, 1,2,3, 11,12,13, 21,22,23, 31,32,33, 111,112,113, ...
Interpretiert man diese Zahlenreihe als Zahlen im 3+ System
(einem Zahlensystem ohne Ziffer 0 außer für die Zahl 0), so stellt sie
gerade die Reihe der natürlichen Zahlen dar. Ein Iris-Koordinatensystem
ist also wie der Zahlenstrahl eine geometrische Darstellung der
natürlichen Zahlen: Die Zahlen sind in Schalen aufgelistet:
Der Zahl 0 entspricht Schale 0, ansonst liegen Zahlen mit 1 Ziffer in
Schale 1, Zahlen mit 2 Ziffern in Schale 2, usw. Der Vervielfältigungsfaktor
repräsentiert die Basis des Zahlensystems.
Verwendet man zur Sektornummerierung ein "normales" Zahlensystem,
das die Ziffer 0 verwendet, so treten manche Zahlen doppelt auf:
Z.B. ist Sektor 001 ungleich Sektor 1, aber die Zahlenwerte sind gleich.
Das kann man so vermeiden: Schale 1 hat 3 Sektoren mit Nummern 1-3,
jede Schale weiter außen hat Vervielfältigungsfaktor 4 mit Sektornummern
0-3. Jetzt beginnt keine Sektornummer (außer 0 selbst) mehr mit 0,
und die Sektornummern, als Zahlen im 4er-System
aufgefaßt, durchlaufen alle natürlichen Zahlen.
Entsprechend könnte man Schale 1 in Sektor 1-4 teilen, dann fortlaufend
in Sektoren 0-4 (ergibt fortlaufende Numerierung im Fünfersystem);
oder Schale 1 in Sektor 1-8, dann in Sektoren 0-8 (ergibt
fortlaufende Numerierung im Neunersystem).
Auch negative Zahlen könnte man als Iris-Koordinaten darstellen,
indem man z.B. Schale 1 in die 6 Sektoren 1, 2, 3, -3, -2, -1 teilt und
dann fortlaufend in je 3 Sektoren unterteilt (oder je 4 Sektoren).
Verwendung: Rechenhilfsmittel, Kugelrechner, Uhr
Man kann ein Iris-Koordinatensystem als Draufsicht auf einen Kegel
(oder einen kegelförmigen Vulkan) mit ringförmigen Höhenstufen ansehen:
Schale 0 entspricht dem Krater, jede weitere Schale
liegt etwas tiefer außen um den Kegel herum. Eine Kugel, die
aus dem Krater rollt, durchläuft auf ihrem Weg abwärts
alle Sektoren und damit alle natürlichen Zahlen. (Voraussetzung:
im letzten Sektor jeder Schale ist eine Lücke, so daß die Kugel
in den 1. Sektor der nächsttieferen Schale fallen kann. Die Kugel
rollt besser, wenn die Schalen nicht konzentrische Ringe bilden,
sondern eine einzige große Spirale, die stetig abwärts läuft.)
Umgekehrt durchläuft bei einem trichterförmigen Modell
(umgedrehter Kegel, 0 liegt ganz unten im Trichter) eine
vom oberen Rand nach innen-unten losrollende Kugel ab einer
bestimmten Zahl alle Zahlen bis zur 0.
Solche Gebilde könnte man in Kugelrechnern
verwenden, mechanischen Rechenmaschinen mit rollenden Kugeln.
Vorteilhaft ist dabei, daß man pro Zahl nur 1 Kugel benötigt.
Eine Kugel im Sektor 222 repräsentiert eben die Zahl 222.
Im selben Sektor könnte man mit einer anderen Kugel (Größe, Gewicht, Farbe)
die Zahl -222 darstellen, mit noch anderen Kugeln die Zahlen
0,222 oder -0,222.
Könnte man die Kugel sehr langsam rollen lassen (besser z.B.
jede Minute von einem Sektor in den nächsten fallen lassen)
hätte man eine Digitaluhr. Abzulesen wäre sie aber nur dann
einfach, wenn bei der Zeiteinteilung und der Unterteilung des
Koordinatensystems dasselbe Zahlensystem verwendet würde.
Dann wäre auch eine LCD-Uhr denkbar mit einem Zifferblatt
in Form von Iris-Koordinaten: Die Zeit wäre dann nicht nur
am einzelnen Sektor ablesbar, sondern von weitem erkennbar
an der Füllung des Zifferblatts von Sektor 0 bis zu diesem
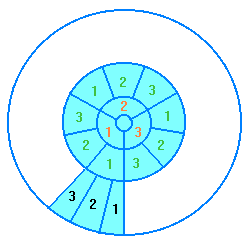
Sektor einschließlich. Bild unten zeigt die Uhrzeit 113:
Alle bereits durchlaufenen Sektoren sind blau gefärbt.
Man könnte den nächsten Sektor, der gerade "abläuft"
(Sektor 121, nicht eingezeichnet), besonders kennzeichnen
(z.B. heller blau, schraffiert blau, oder auffällig rot),
doch erscheint das unnötig.
Verwendung: Wortraum
Zur Bezeichnung von Sektoren kann man statt Zahlen auch Buchstaben
verwenden (und sogar mit ihnen rechnen). Angenommen, wir hätten eine
künstliche Sprache mit einem regelmäßigen Lautsystem, beispielsweise:
8 Konsonanten: s f t p n m l v
8 Vokalphoneme: i y e ei a ai o oi
Nun verwenden wir zur Sektor-Nummerierung statt Ziffern abwechselnd
Konsonanten (in den Schalen 1,3,5 ...) und Vokale (in den Schalen
2,4,6 ...), und zwar entsprechend ihrer Position im ABC.
(Der bisherige Sektor 0 erhält das Leerzeichen zugeordnet, oder
man läßt ihn einfach weg.) Das Koordinatensystem sieht jetzt so aus:
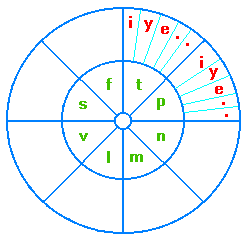
Die Sektornummern lauten jetzt beispielsweise s, si, sis, sasa, nina
oder ähnlich. Allgemein: sie sind eine regelmäßige Folge Konsonant +
Vokal + Konsonant ... Bei Sprachen, deren Wörter nur diese Struktur
haben, entspricht somit jedes Wort einer Position, und beim Durchlaufen
aller Sektoren vom Zentrum aus werden alle bildbaren Worte durchlaufen.
(Man könnte ähnlich wie bei der Buchstaben-Lautbildschrift
den Vokal i nur als phonetischen Füllvokal verwenden und ihn am Wortende
sprechen, wenn das Wort sonst mit einem Konsonant enden würde. Dann hätten
alle Sektornummern akustisch die Silbenstruktur Konsonant + Vokal.)
Eine Sonderform von Iris-Koordinaten mit Buchstabenbezeichnungen und
Vervielfältigungsfaktor 1 ist folgendes System:
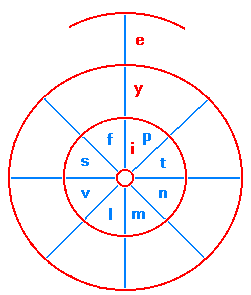
Hier geben die Konsonanten nur den Drehwinkel, die Vokale nur die
Entfernung, also die Schalen-Nummer, an. Ähnlich wie bei Notenschrift
gilt hier: je weiter vom Zentrum, desto tiefer der Ton.
Verwendung: Ortsplan
Man könnte ein Iris-Koordinatensystem auch als Ortsplan
(Ortsgrundriß) verwenden. Die Linien wären Straßen, Sektor 0
wäre ein Platz in der Mitte, andere Sektoren wären Parks,
Wohn-, Einkaufs- oder Büroblocks.
Straßennamen wären aber ergonomischer als Sektornummerierung. Doch
könnte man radiale Straßen ringsherum alphabetisch benennen, mit
kurzen Namen für kurze Straßen, langen Namen für lange Straßen.
Hier lassen sich viele Systeme austüfteln.
Bewertung
Iris-Koordinaten erlauben eine einfache Positionsangabe in der
Ebene von einem festen Zentrum aus (Gelände, Planetensystem, s.o.).
Vielleicht sind sie für einige Spezialzwecke optimal.
Ansonsten sind sie interessant, aber weniger praxistauglich
als z.B. kartesische Koordinaten.
Nachteilig ist: Iris-Koordinaten
widerspiegeln den Zahlenraum nur, wenn entweder die weniger praktischen
Plus-Zahlensysteme zur Numerierung verwendet werden, oder wenn der
Teilungsfaktor in Schale 1 um 1 kleiner ist als bei den äußeren Schalen.
Sektoren verschiedener Schalen haben etwas ungleiche Form.
Eine Verfeinerung der Positionsangabe durch Nachkommastellen
macht die Sache geometrisch komplizierter.
Bei dem auf ein Zentrum bezogenen Gradnetz läßt sich die Position
bzgl. einem anderen Mittelpunkt nicht ablesen.
Diese Nachteile vermeiden die ähnlichen Raster-Koordinaten.
Die Benutzung der hier beschriebenen Techniken ist frei Stand: 12.2.04
Autor und Erfinder: Leonhard Heinzmann Homepage