Raster-Koordinatensystem: Variationen

Autor  und  Erfinder:    Leonhard  Heinzmann                   Stand:  1.3.02

Vor diesem Artikel sollte man den über das allgemeine Raster-Koordinatensystem gelesen haben.

Variation: Exzentrischer 9-Quadrat-Raster

Man kann eine halbe Ebene adressieren, indem man in einem Neunerblock (im Bild grün) das Quadrat Mitte-unten als Nullquadrat definiert, und in jeder weiteren Stufe links, oben und rechts weitere 8 Quadrate (im Bild weiß) hinzufügt.   Optimal für die Adressierung ist hier das 9-er System (Ziffern 0-8).





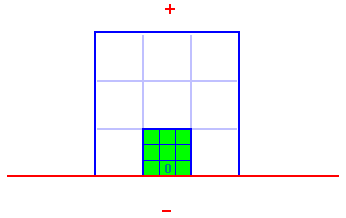
Man kann auch die andere Hälfte der Ebenen adressieren (im Bild unterhalb der roten Linie), indem man obige Neunerblocks nach unten spiegelt und ihre Sektornummern mit Minuszeichen versieht.

Man kann Quadrat 0 auch in eine Ecke legen, z.B. links unten. Doch ist dann das unten beschriebene 4-Quadrat-Raster wohl vorzuziehen, weil einfacher.


Ähnlich ist ein 6-Quadrat-Raster möglich, wobei aber die Quadrate dann zu immer flacheren Rechtecken werden.   Optimal für die Adressierung ist hier das 6-er System (Ziffern 0-5).

Variation: 4-Quadrat-Raster

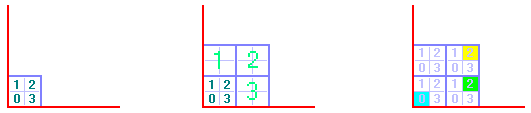
Ähnlich kann man ein 4-Quadrat-Koordinatensystem entwerfen: Quadrat 0 liegt nun in einer Ecke, 3 andere Quadrate mit Nummern 1-3 liegen viertelkreisförmig um es herum (Bild unten, links).
In der nächsthöheren Größenstufe werden 3 weitere solche Viererblocks hinzugefügt (Bild unten, Mitte. Aus Platzgründen fehlen im großen Quadrat links unten die große grüne 0, in den anderen großen Quadraten die Nummerierung der kleinen Quadrate.)
Zur Verdeutlichung sind im Bild unten rechts alle kleinen Quadrate mit ihren lokalen Nummern dargestellt. Das blaue Quadrat hat die Gesamtadresse 00 = 0, das gelbe 22, das grüne 32.





So ist schrittweise eine Viertelebene (1 Quadrant) adressierbar, sie repräsentiert alle positiven Zahlen (wenn man die Adressen als Zahlen im Vierersystem betrachtet).
Man kann die ganze Ebene adressieren, wenn man alle 4 Quadranten einzeln wie oben adressiert. Zur Unterscheidung enthält jeder Quadrant ein Vorzeichen: + oder - oder + i oder - i. Die ganze Ebene bzw. das ganze Koordinatensystem repräsentiert dann die komplexen Zahlen, das mächtigste Zahlensystem:





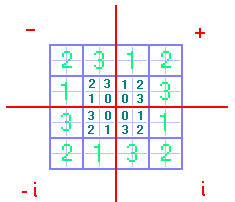
Die Nummerierung der kleinen Quadrate ist in jedem Quadranten gegenüber dem vorigen um 90 Grad gedreht: Dann liegt 0 immer innen (Richtung Achsenkreuzung), und es gilt, von der 0 nach außen blickend: 1=links, 2= mitte, 3= rechts. Doch könnte man auch alle Viererblocks kleiner Quadrate exakt gleich numerieren. Optimal für die Adressierung ist immer das 4-er System (Ziffern 0-3).

Variation: 4-Dreieck-Raster

Hier ist wieder eine symmetrische Lösung möglich, das heißt Dreieck 0 liegt in der Mitte (von insgesamt 4 Dreiecken, im Bild grün). In der nächsten Stufe werden um das Gesamtdreieck 3 weitere Dreiecke (grüne Nummern) herumgelegt. In der nächsten Stufe dann wieder 3 (im Bild ohne Nummern).





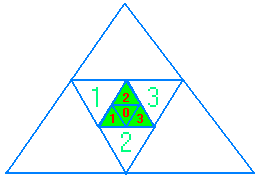
Bei jedem Stufenwechsel klappt das Gesamtdreieck vertikal um (seine Spitze ist abwechselnd oben oder unten). Die Nummerierung der neuen Dreiecke kann deshalb auf 2 Arten erfolgen: entweder so, daß immer gilt: 1= links, 2 = mitte, 3 = rechts (wie im Bild). Oder so, daß der Drehsinn der Zahlen erhalten bleibt. Optimal für die Adressierung ist immer das 4-er System (Ziffern 0-3).
Gleichseitige Dreiecke erscheinen am zweckmäßigsten, doch funktioniert dieses Koordinatensystem auch noch mit gleichschenkligen Dreiecken.

Dieses Koordinatensystem wirkt bereits reichlich exotisch. Doch wären auch dafür Anwendungsgebiete denkbar, z.B. bei der Modellierung beliebiger Formen durch Dreiecke (die vor der Darstellung auf dem Bildschirm gerundet werden), was heutzutage das Standardverfahren ist.

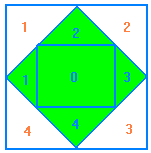
Variation: Drehquadrat-Raster

Das Nullelement ist ein Quadrat. Drumherum werden 4 gleichschenklige rechtwinklige Dreiecke (mit Sektornummern 1-4) so gelegt, daß sich wieder ein Quadrat ergibt (grüne Fläche im Bild). Das läßt sich endlos fortsetzen (die nächsten 4 Dreiecke sind im Bild weiß, Sektor 0 dieses weißen Quadrats ist das große grüne Quadrat).
Der Vorgang läßt sich auch interpretieren als Herumlegen eines um 90 Grad gedrehten Quadrats um das bisherige, mit Seitenlänge = Diagonale des alten Quadrats).





Das Quadrat 0 der jeweiligen Ebene ist bei aufeinanderfolgenden Ebenen jeweils um 90 Grad gedreht. Man kann die Sektornummern 1-4 vollständig rotieren lassen (in 4 Stufen also um 360 Grad) oder nach je 2 Stufen wieder zur alten Numerierung zurückkehren.
Optimal für die Adressierung ist das 5-er System (Ziffern 0-4).

Auch nach innen läßt sich diese Aufteilung der Quadrate fortführen, d.h. die kleinsten Quadrate lassen sich weiter so unterteilen (die resultierenden Sektoren haben Nummern mit Nachkommastellen). Die Dreiecke müssen aber nach einer anderen Methode, z.B. dem 4-Dreieck-Raster, aufgeteilt werden. Man hat nun einen gemischten Raster mit 2 Formen und 2 Teilungsfaktoren: 5 bei Quadraten, 4 bei den Dreiecken.

Variation: 7-Kreise-Raster

Ein Raster-Koordinatensystem kann auch auf Kreisen basieren: Um einen Mittelkreis werden 6 weitere Kreise gelegt (im Bild alle blau). Dieses "Bündel" wird dann als neuer Kreis betrachtet, um den 6 weitere Kreise derselben Größe gelegt werden (im Bild rot). Diese enthalten alle dieselbe Unterteilung in kleine Kreise wie der Mittelkreis (nur bei diesem eingezeichnet).





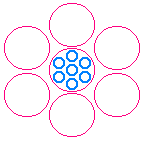
Im Gegensatz zu obigen Koordinatenrastern bleiben hier Lücken zwischen den einzelnen Grundelementen (hier Kreisen) derselben Adressierungsstufe. (Würde man weniger oder mehr als 6 Kreise um den Mittelkreis legen, wäre dieser Effekt noch stärker.) Doch ist es möglich, alle Kreise etwas größer zu machen, so daß sie sich überlappen und die Position jedes Punktes beliebig genau angegeben werden kann.
Vergleiche hierzu die ähnlichen Iris-Koordinaten

Als Anwendungsgebiet wären hier die Bahnen von Planeten und ihren Monden denkbar, doch sind diese etwas unregelmäßiger. Das Bild erinnert an eine Blume oder einen Zellhaufen - vielleicht ist dieses Koordinatensystem biologisch anwendbar: dort ist nicht die absolute Position entscheidend, sondern die relative z.B. die Lage einer Zelle in einem Zellbündel.

Optimal für die Adressierung ist hier das 7-er System (Ziffern 0-6).

Weitere Variationen

Es sind viele weitere Variationen möglich, der Kreativität sind hier fast keine Grenzen gesetzt. Prädestiniert sind Formen, die 2 Bedingungen erfüllen:

- Durch Anlagern einer festen Anzahl gleicher Formen ergibt sich wieder dieselbe Form
- Diese Formen füllen den Raum vollständig aus (Parkettierung)

Doch sind auch Ausnahmen möglich:   Ausnahme zu Regel 1 ist z.B. der Drehquadrat-Raster, zu Regel 2 der 7-Kreis-Raster.
Möglich sind auch periodisch in Form und / oder Zahl variierende Raster.

Räumliche Raster

Obige Raster-Koordinatensysteme der Ebene sind analog auch im Raum mit 3 und mehr Dimensionen möglich. Im übergeordneten Artikel wurde dies bereits für das 9-Quadrat-Raster beschrieben, das im 3-dimensionalen Raum zu einem Würfel mit 3*3*3 = 27 untergeordneten Würfeln wird.

Allgemein nimmt dabei die Anzahl der Teilsektoren pro Sektor meist zu. Dann ist zur Sektornummerierung ein anderes Zahlensystem optimal, außer wenn die neue Anzahl Teilsektoren gleich einer Potenz der alten ist.